题目内容
15.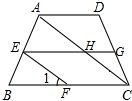 如图,AD∥EG∥BC,AC∥EF,若∠1=50°,则∠AHG=130°.
如图,AD∥EG∥BC,AC∥EF,若∠1=50°,则∠AHG=130°.
分析 由平行线的性质可得到∠1=∠HEF=∠AHE=∠GHC=∠HCF=∠DAC,结合∠DAH+∠AHG=180°,可求得∠AHG.
解答 解:∵EF∥AC,
∴∠1=∠HCF,∠FEH=∠AHE,
∵EG∥BC,
∴∠1=∠FEH,∠GHC=∠HCF,
∴AD∥BC,
∴∠DAH=∠HCF,
∴∠1=∠HEF=∠AHE=∠GHC=∠HCF=∠DAC,
∵∠1=50°,
∴∠DAC=∠1=50°,
∵AD∥EG,
∴∠DAC+∠AHG=180°,
∴∠AHG=180°-50°=130°;
故答案为:130.
点评 本题主要考查平行线的性质,掌握平行线的性质是解题的关键,即①两直线平行?同位角相等,②两直线平行?内错角相等,③两直线平行?同旁内角互补.

练习册系列答案
相关题目
5.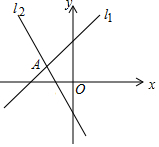 如图,在直角坐标系中,直线l1:y1=kx+b与直线l2:y2═mx+n在第二象限相交于点A(-1,a),则不等式kx+b<mx+n的解集是( )
如图,在直角坐标系中,直线l1:y1=kx+b与直线l2:y2═mx+n在第二象限相交于点A(-1,a),则不等式kx+b<mx+n的解集是( )
 如图,在直角坐标系中,直线l1:y1=kx+b与直线l2:y2═mx+n在第二象限相交于点A(-1,a),则不等式kx+b<mx+n的解集是( )
如图,在直角坐标系中,直线l1:y1=kx+b与直线l2:y2═mx+n在第二象限相交于点A(-1,a),则不等式kx+b<mx+n的解集是( )| A. | x<-1 | B. | x<a | C. | x>-1 | D. | -1<x<0 |
10.某校乐器社团成员的年龄有12,13,14,15四种,统计结果如下表:
根据表中信息判断该校乐器社团成员的平均年龄为14岁.
| 年龄/岁 | 12 | 13 | 14 | 15 |
| 人数/人 | 2 | 4 | 6 | 8 |
7.下列图案是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
4.下列运算正确的是( )
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | 2$\sqrt{3}$×$3\sqrt{3}$=6$\sqrt{3}$ | C. | $\sqrt{2}$$÷\sqrt{3}$=$\frac{\sqrt{6}}{3}$ | D. | 5$\sqrt{5}$-2$\sqrt{2}$=3$\sqrt{3}$ |
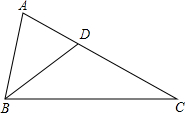 如图,已知BD是∠ABC的角平分线,且∠C=∠DBC,∠BDA=72°,求△ABC各内角度数.
如图,已知BD是∠ABC的角平分线,且∠C=∠DBC,∠BDA=72°,求△ABC各内角度数.