题目内容
8．若二次函数y=ax2+bx+c（a≠0）的图象上有两点，坐标分别为（x1，y1），（x2，y2），其中x1＜x2，y1y2＜0，则下列判断正确的是（ ）| A． | a＜0 | |
| B． | a＞0 | |
| C． | 方程ax2+bx+c=0必有一根x0满足x1＜x0＜x2 | |
| D． | y1＜y2 |
分析 判断出抛物线与x轴有一个交点在两个点之间，然后根据二次函数与方程的关系求解即可．
解答 解：∵x1＜x2，y1y2＜0，
∴两个交点在x轴的上方一个，下方一个，
∴抛物线与x轴有一个交点在这两个点之间，
∴方程ax2+bx+c=0必有一根x0满足x1＜x0＜x2．
a的正负情况以及y1与y2哪一个是正数哪一个是负数无法判断．
故选C．
点评 本题考查了二次函数图象上点的坐标特征，熟练掌握二次函数图象的特征并判断出抛物线上的两个点与x轴的关系是解题的关键．
练习册系列答案
核心素养学练评系列答案
单元期中期末卷系列答案
相关题目
如图是我国古代数学家赵爽在为《周髀算经》作注解时给出的“弦图”，它解决的数学问题是勾股定理．
如图：在矩形ABCD中，AD=$\sqrt{2}$AB，∠BAD的平分线交BC于点E，DH⊥AE于点H，连接BH并延长交CD于点F，连接DE交BF于点O，有下列结论：①∠AED=∠CED；②OE=OD；③△BEH≌△HDF；④BC-CF=2EH；⑤AB=FH．其中正确的结论有（ ）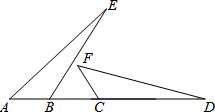
如图，点A，B，C，D在同一条直线上，AB=FC，∠A=∠F，∠EBC=∠FCB．求证：BE=CD．
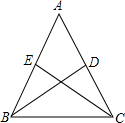如图，在△ABC中，AB=AC，点E，D分别在AB，AC上，不再添加其他辅助线，添加一个条件AE=AD，使BD=CE（只添一个即可）．
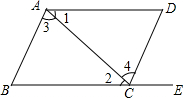如图，给出下列条件：