题目内容
19. 如图:在矩形ABCD中,AD=$\sqrt{2}$AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,有下列结论:①∠AED=∠CED;②OE=OD;③△BEH≌△HDF;④BC-CF=2EH;⑤AB=FH.其中正确的结论有( )
如图:在矩形ABCD中,AD=$\sqrt{2}$AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,有下列结论:①∠AED=∠CED;②OE=OD;③△BEH≌△HDF;④BC-CF=2EH;⑤AB=FH.其中正确的结论有( )| A. | 5个 | B. | 4个 | C. | 3个 | D. | 2个 |
分析 先证明△ABE和△ADH等腰直角三角形,得出AD=AE,AB=AH=DH=DC,得出∠ADE=∠AED,即可得出①正确;先证出OE=OH,同理:OD=OH,得出OE=OD,②正确;由ASA证出△BEH≌△HDF,得出③正确;过H作HK⊥BC于K,可知KC=$\frac{1}{2}$BC,HK=KE,得出$\frac{1}{2}$BC=HK+HE,BC=2HK+2HE=FC+2HE,得出④正确;由AB=AH,∠BAE=45°,得出△ABH不是等边三角形,AB≠BH,即AB≠HF,故⑤错误.
解答 解:∵四边形ABCD是矩形,
∴∠BAD=∠ABC=∠C=∠ADC=90°,AB=DC,AD∥BC,
∴∠ADE=∠CED,
∵∠BAD的平分线交BC于点E,
∴∠BAE=∠DAH=45°,
∴△ABE和△ADH是等腰直角三角形,
∴AE=$\sqrt{2}$AB,AD=$\sqrt{2}$AH,
∵AD=$\sqrt{2}$AB=$\sqrt{2}$AH,
∴AD=AE,AB=AH=DH=DC,
∴∠ADE=∠AED,
∴∠AED=∠CED,
∴①正确;
∵∠DAH=∠ADH=45°,
∴∠ADE=∠AED=67.5°,
∵∠BAE=45°,
∴∠AHB=∠ABH=67.5°,
∴∠OHE=67.5°,
∴∠OHE=∠AED,
∴OE=OH,
同理:OD=OH,
∴OE=OD,
∴②正确;
∵∠ABH=∠AHB=67.5°,
∴∠HBE=∠FHD,
在△BEH和△HDF中,$\left\{\begin{array}{l}{∠HEB=∠FDH=45°}&{\;}\\{BE=DH}&{\;}\\{∠HBE=∠FHD}&{\;}\end{array}\right.$,
∴△BEH≌△HDF(ASA),
∴③正确;
BC-CF=2HE正确,过H作HK⊥BC于K,
可知KC=$\frac{1}{2}$BC,HK=KE,
由上知HE=EC,
∴$\frac{1}{2}$BC=KE十Ec,
又KE=HK=$\frac{1}{2}$FC,HE=EC,
故$\frac{1}{2}$BC=HK+HE,BC=2HK+2HE=FC+2HE
∴④正确;
⑤∵AB=AH,∠BAE=45°,
∴△ABH不是等边三角形,
∴AB≠BH,
∴即AB≠HF,故⑤不正确;
故选:B.
点评 本题考查了全等三角形的判定与性质、矩形的性质、角平分线的性质以及等腰直角三角形的判定与性质;证明三角形全等和等腰直角三角形是解决问题的关键.

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
| A. | 10 | B. | 18 | C. | 20 | D. | 22 |
| A. | 有一个实根 | B. | 有两个不相等的实根 | ||
| C. | 有两个相等的实根 | D. | 无解 |
| A. | 2或-5 | B. | -2或5 | C. | 2或5 | D. | -2或-5 |
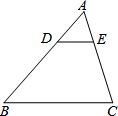 如图,在△ABC中,点D、E分别在AB、AC边上,DE∥BC,若AD=1,BD=2,则$\frac{DE}{BC}$的值为( )
如图,在△ABC中,点D、E分别在AB、AC边上,DE∥BC,若AD=1,BD=2,则$\frac{DE}{BC}$的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{9}$ |
| A. | a<0 | |
| B. | a>0 | |
| C. | 方程ax2+bx+c=0必有一根x0满足x1<x0<x2 | |
| D. | y1<y2 |
| A. | 抛一枚硬币,正面朝上 | |
| B. | 黑暗中从5把不同的钥匙中随意摸出一把,用它打开了门 | |
| C. | 打开电视机,任选一个频道,屏幕上正在播放新闻联播 | |
| D. | 4个人分成3组,其中一组必有2人 |
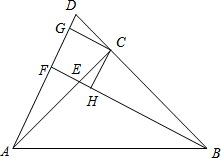 已知:如图,在Rt△ABC中,∠ACB=90°,AC=BC,点E在边AC上,延长BC至D点,使CE=CD,延长BE交AD于F,过点C作CG∥BF,交AD于点G,在BE上取一点H,使∠HCE=∠DCG.
已知:如图,在Rt△ABC中,∠ACB=90°,AC=BC,点E在边AC上,延长BC至D点,使CE=CD,延长BE交AD于F,过点C作CG∥BF,交AD于点G,在BE上取一点H,使∠HCE=∠DCG.