题目内容
9.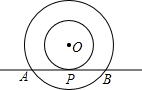 如图,以点O为圆心的两个同心圆中,大圆的弦AB切小圆于点P.
如图,以点O为圆心的两个同心圆中,大圆的弦AB切小圆于点P.(1)PA与PB相等吗?请说明理由;
(2)若AB=8,求圆环的面积.
分析 (1)PA=PB,连接OP,在大圆中利用垂径定理即可证明,
(2)连接OA,根据切线的性质和勾股定理可得:OA2-OP2=$\frac{1}{2}$AB2,写出环形的面积表达式,把数值代入即可.
解答 解:
(1)PA=PB,理由如下:
连接OP,
∵大圆的弦AB切小圆于点P,
∴OP⊥AB,
∴PA=PB,
(2)接OA,
∵大圆中长为8的弦AB与小圆相切,
∴OP⊥AB,AP=4,
∴OA2-OP2=16,
∴πOA2-πOP2=(OA2-OP2)π,
∴圆环的面积=16π.
点评 本题考查了切线的性质、垂径定理以及勾股定理的运用,熟记和圆的各种定理是解题的关键.

练习册系列答案
相关题目
17.计算$\frac{1}{a}$×(-a)÷(-$\frac{1}{a}}$)×a等于( )
| A. | 1 | B. | a2 | C. | -a | D. | $\frac{1}{a^2}$ |
 如图,两根旗杆间相距12m,某人从点B沿BA走向点A,一段时间后他到达点M,此时他仰望旗杆的顶点C和D,两次视线的夹角为90°,且CM=DM.已知旗杆AC的高为3m,该人的运动速度为1m/s,则这个人运动到点M所用时间是3s.
如图,两根旗杆间相距12m,某人从点B沿BA走向点A,一段时间后他到达点M,此时他仰望旗杆的顶点C和D,两次视线的夹角为90°,且CM=DM.已知旗杆AC的高为3m,该人的运动速度为1m/s,则这个人运动到点M所用时间是3s.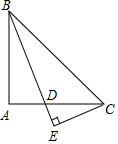 已知:△ABC是等腰直角三角形,∠BAC=90°,BD平分∠ABC交AC于点D,CE垂直于BD,交BD的延长线于点E,求证:BD=2CE.
已知:△ABC是等腰直角三角形,∠BAC=90°,BD平分∠ABC交AC于点D,CE垂直于BD,交BD的延长线于点E,求证:BD=2CE.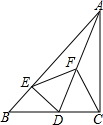 如图,在Rt△ABC中,∠ACB=90°,D是边BC上一动点(不与B,C重合),DE⊥AB于点E,点F是线段AD的中点,连接EF,CF.
如图,在Rt△ABC中,∠ACB=90°,D是边BC上一动点(不与B,C重合),DE⊥AB于点E,点F是线段AD的中点,连接EF,CF.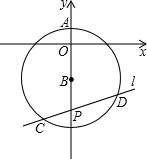 如图,圆心在y轴的负半轴上,半径为5的⊙B与y轴的正半轴交于点A(0,1),过点P(0,-7)的直线l与⊙B相交于C,D两点,则弦CD长的所有可能的整数值有3个.
如图,圆心在y轴的负半轴上,半径为5的⊙B与y轴的正半轴交于点A(0,1),过点P(0,-7)的直线l与⊙B相交于C,D两点,则弦CD长的所有可能的整数值有3个.