题目内容
1.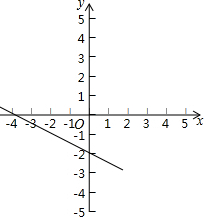 如图,
如图,(1)求直线解析式;
(2)点(-2,-1)、(4,-3)是否在该直线上?
(3)求直线上到y轴距离等于5的点的坐标.
分析 (1)根据图示知,该函数图象经过点(-4,0)、(0,-2).把它们分别代入函数解析式y=kx+b(k≠0),列出关于系数k、b的方程组,通过解方程即可求得它们的值.
(2)把x=-2和x=4代入解析式即可判断.
(3)根据直线上的点到y轴距离是5,故x=±5,求出y的值即可得出结论.
解答 解:(1)设直线l的解析式是y=kx+b(k≠0).
如图所示,该函数图象经过点(-4,0)、(0,-2),则$\left\{\begin{array}{l}{-4k+b=0}\\{b=-2}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=-2}\end{array}\right.$.
故该直线的解析式为:y=-$\frac{1}{2}$x-2.
(2)把x=-2代入得,y=-$\frac{1}{2}$×(-2)-2=-1,
把x=4代入得,y=-$\frac{1}{2}$×4-2=-4≠-3,
∴点(-2,-1)在该直线上,点E(4,-3)不在该直线上.
(3)∵直线上的点到y轴距离是5,
∴x=±5,
当x=5时,即y=-$\frac{1}{2}$×5-2=-$\frac{9}{2}$;
当y=-5时,即y=-$\frac{1}{2}$×(-5)-2=$\frac{1}{2}$.
∴符合条件的点的坐标为:(5,-$\frac{9}{2}$)或(-5,$\frac{1}{2}$).
点评 本题考查了待定系数法求一次函数的解析式以及一次函数图象上点的坐标特征,熟练掌握待定系数法是解题的关键.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
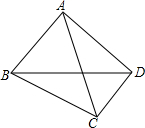 如图,四边形ABCD中,∠BAC=∠BCD=90°,若AC平分∠BCD,求证:AB=AD.
如图,四边形ABCD中,∠BAC=∠BCD=90°,若AC平分∠BCD,求证:AB=AD. 如图,假设三角形ABC的面积为1平方分米,且BE=2EC,F是CD的中点.那么,阴影部分的面积是多少分米?
如图,假设三角形ABC的面积为1平方分米,且BE=2EC,F是CD的中点.那么,阴影部分的面积是多少分米?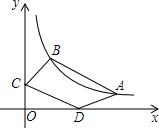 在反比例函数y=$\frac{8}{x}$(x>0)的图象上有不重合的A、B两点,A点横坐标为8,B点横坐标为4.求:
在反比例函数y=$\frac{8}{x}$(x>0)的图象上有不重合的A、B两点,A点横坐标为8,B点横坐标为4.求: 在△ABC中,∠B=60°,AD⊥BC,垂足为D,若AD=3cm,AC=5cm,求△ABC的面积.
在△ABC中,∠B=60°,AD⊥BC,垂足为D,若AD=3cm,AC=5cm,求△ABC的面积.