题目内容
6.一项工程,甲独做要x小时,乙独做要y小时,两人合作完成这项工程的时间为$\frac{xy}{x+y}$小时.分析 把这项工程看作单位“1”,利用工作总量÷工作效率和=工作时间列式解答即可.
解答 解:1÷($\frac{1}{x}$+$\frac{1}{y}$)
=1÷$\frac{x+y}{xy}$
=$\frac{xy}{x+y}$(小时).
故答案为:$\frac{xy}{x+y}$.
点评 此题考查了列代数式;解题的关键是正确运用工作量、工作效率、工作时间之间的关系解决问题.

练习册系列答案
相关题目
17.某企业组织员工外出旅游,原计划租用28座客车若干辆,但有4人没座位;若租用同样数量的33座客车,只有一辆空余了16个座位,其他车辆都坐满,该企业外出旅游的员工有( )
| A. | 108人 | B. | 112人 | C. | 116人 | D. | 120人 |
18.某市自来水供水公司为鼓励企业节约用水,按如表规定收取水费,某企业十二月份共缴水费128元,则十二月份用水( )
| 用水量 | 单价(元/吨) |
| 不超过40吨的部分 | 2 |
| 超过40吨的部分 | 2.4 |
| A. | 55吨 | B. | 60吨 | C. | 65吨 | D. | 70吨 |
16.已知y关于x的函数表达式为:y=x+$\frac{1}{x}$(x>0).
(1)请你补全表格.
(2)利用上述表格.在图表格中画出该函数的大致图象.
(3)仔细观察该图象.请你概括出该函数的两个不同性质的特征.

(1)请你补全表格.
| x | … | $\frac{1}{3}$ | $\frac{1}{2}$ | 1 | 2 | 3 | 4 | … |
| y | … | $\frac{10}{3}$ | $\frac{5}{2}$ | 2 | $\frac{5}{2}$ | $\frac{10}{3}$ | $\frac{17}{4}$ | … |
(3)仔细观察该图象.请你概括出该函数的两个不同性质的特征.

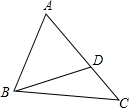 如图,D是△ABC的边AC上的一点,连接BD,已知AB=6,AD=4,CD=5.求证:∠ABD=∠C.
如图,D是△ABC的边AC上的一点,连接BD,已知AB=6,AD=4,CD=5.求证:∠ABD=∠C. 如图,
如图,