题目内容
10.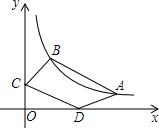 在反比例函数y=$\frac{8}{x}$(x>0)的图象上有不重合的A、B两点,A点横坐标为8,B点横坐标为4.求:
在反比例函数y=$\frac{8}{x}$(x>0)的图象上有不重合的A、B两点,A点横坐标为8,B点横坐标为4.求:(1)A、B两点的坐标;
(2)若C(0,2)、D(3,0)两点也在同一坐标平面内,求四边形ABCD的面积.
分析 (1)把横坐标代入解析式即可求得纵坐标,从而求得A、B两点的坐标;
(2)用四边形所在的矩形的面积减去四周三个直角三角形的面积列式计算即可得解.
解答 解:(1)∵A点横坐标为8,B点横坐标为4.
∴把x=8代入求得y=$\frac{8}{8}$=1,把x=4代入求得y=$\frac{8}{4}$=2,
∴A(8,1),B(4,2).
(2)∵A(8,1)、B(4,2)、C(0,2)、D(3,0),
∴S四边形ABCD=8×2-$\frac{1}{2}$×2×3-$\frac{1}{2}$×5×1-$\frac{1}{2}$×3×4=$\frac{9}{2}$.
点评 本题考查了反比例函数图象上点的坐标特征,三角形的面积,难点在于(2)把不规则四边形转化为规则的三角形和矩形进行面积计算.

练习册系列答案
相关题目
18.某市自来水供水公司为鼓励企业节约用水,按如表规定收取水费,某企业十二月份共缴水费128元,则十二月份用水( )
| 用水量 | 单价(元/吨) |
| 不超过40吨的部分 | 2 |
| 超过40吨的部分 | 2.4 |
| A. | 55吨 | B. | 60吨 | C. | 65吨 | D. | 70吨 |
20.将一个底面直径是10厘米,高为36厘米的圆柱体锻压成底面直径为20厘米的圆柱体,在这个过程中不改变的是( )
| A. | 圆柱的高 | B. | 圆柱的侧面积 | C. | 圆柱的体积 | D. | 圆柱的底面积 |
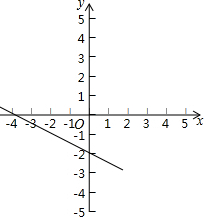 如图,
如图,