题目内容
10.如图1,点C为△MNQ的边QN上一点(QC<CN),点C关于MN、MQ的对称点分别为点A、B,连接AB、BC、AC,且AB经过点M.(1)求证:M为AB的中点;
(2)如图2,连接BQ、AN,求证:BQ∥AN;
(3)如图3,在(2)的条件下,延长AN到R,使NR=BQ.连接BR,BR与QN相交于点O,连接AO、MC,当AO⊥BR,QN=4$\sqrt{3}$时,求MC的长?

分析 (1)连接MC,由轴对称的性质可知BM=MC=MA,从而结论得证;
(2)同样由轴对称性质可知∠BMQ=∠CMQ,∠NMC=∠NMA,∠BQM=∠CQM,∠CNM=∠ANM,于是∠QMN=90°,∠CQM+∠CNM=90°,从而∠BQC+∠ANC=180°,得证;
(3)由(2)中所得结论BQ∥AN以及NR=BQ易证△BQO≌△RNO,从而可得BO=RO,QO=NO,又AO⊥BR,于是AB=AR,连接MO,则MO为△ABR中位线,于是AR=2MO,而MO为Rt△QMN斜边中线,故QN=2MO,得到AB=QN,而CM=$\frac{1}{2}$AB,水落石出.
解答 解:(1)连接MC,如图1,
∵B、C关于MQ对称,
∴BM=CM=MA,
∴M为AB中点;
(2)如图2,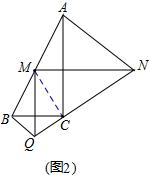
∵B、C关于MQ对称,
∴∠BMQ=∠CMQ,∠BQM=∠CQM,
同理∠NMC=∠NMA,∠CNM=∠ANM,
∴∠QMN=90°,
∴∠CQM+∠CNM=90°,
∴∠BQC+∠ANC=180°,
∴BQ∥AN;
(3)连接MO,如图3,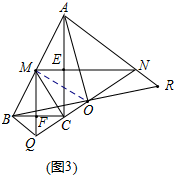
设BC与MQ交于点F,AC与MN交于点E,
∵B、C关于MQ对称,A、C关于MN对称,
∴MQ垂直平分BC,MN垂直平分AC,
∴MFCE为矩形,
∴∠ACB=90°,
∵AN∥BQ,
∴∠ONR=∠OQB,∠ORN=∠OBQ,
在△ONR和△OQB中,
$\left\{\begin{array}{l}{∠ONR=∠OQB}\\{NR=BQ}\\{∠ORN=∠OBQ}\end{array}\right.$,
∴△ONR≌△OQB(ASA),
∴OQ=ON,OB=OR,
∴MO=OQ=ON,
又M为AB中点,
∴MO=$\frac{1}{2}$AR,
∵AO⊥BR,
∴AB=AR,
∵QR=4$\sqrt{3}$,
∴AB=AR=4$\sqrt{3}$,
∴MC=$\frac{1}{2}$AB=2$\sqrt{3}$.
点评 本题为几何变换综合题,主要考查了轴对称的性质、平行线的判定与性质、全等级三角形的判定与性质、矩形的判定与性质、直角三角形斜边中线定理、三角形中位线定理等重要知识点,综合性较强,难度较大.熟练掌握轴对称的性质是解决本题的切入点和关键.

 阅读快车系列答案
阅读快车系列答案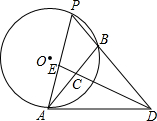 如图,AD切⊙O于A,DBP交⊙O于B,P,C为AB的中点,DC的延长线交AB于E,求证:$\frac{B{D}^{2}}{A{D}^{2}}$=$\frac{AE}{EP}$.
如图,AD切⊙O于A,DBP交⊙O于B,P,C为AB的中点,DC的延长线交AB于E,求证:$\frac{B{D}^{2}}{A{D}^{2}}$=$\frac{AE}{EP}$. △OA1B1,△B1A2B2,△B2A3B3…均为等腰直角三角形,依次如图方式放置,点A1、A2、A3和B1、B2、B3分别在直线y=x+2和x轴上,则An的坐标为An(2n-2,2n).
△OA1B1,△B1A2B2,△B2A3B3…均为等腰直角三角形,依次如图方式放置,点A1、A2、A3和B1、B2、B3分别在直线y=x+2和x轴上,则An的坐标为An(2n-2,2n). 一只蚂蚁从点A沿数轴向右爬2个单位到达点B,点A表示-$\sqrt{2}$,设点B所表示的数为m,则|m-1|+|m+1|的值为2.
一只蚂蚁从点A沿数轴向右爬2个单位到达点B,点A表示-$\sqrt{2}$,设点B所表示的数为m,则|m-1|+|m+1|的值为2. 如图,在A、B两处之间要修一条笔直的公路,从A地测得公路走向是北偏东46°,公司要求A、B两地同时开工,并保证若干天后公路准确接通.
如图,在A、B两处之间要修一条笔直的公路,从A地测得公路走向是北偏东46°,公司要求A、B两地同时开工,并保证若干天后公路准确接通.