题目内容
15.关于x的一元二次方程(m-$\sqrt{3}$)x2+x+2m2-6=0的一个根为0,则m的值为-$\sqrt{3}$.分析 根据一元二次方程的定义得到m-$\sqrt{3}$≠0,由方程的解的定义,把x=0代入已知方程,列出关于m的新方程,通过解新方程来求m的值.
解答 解:∵关于x的一元二次方程(m-$\sqrt{3}$)x2+x+2m2-6=0的一个根为0,
∴2m2-6=0,且m-$\sqrt{3}$≠0,
∴m=±$\sqrt{3}$,且m-$\sqrt{3}$≠0,
解得,m=-$\sqrt{3}$,
故答案是:-$\sqrt{3}$.
点评 本题考查了一元二次方程的解的定义和一元二次方程的定义.注意二次项系数不等于零.

练习册系列答案
相关题目
6.满足$-\sqrt{2}$<x<$\sqrt{5}$的整数x的个数( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |

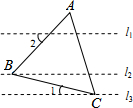 如图,直线l1∥l2∥l3,等边△ABC的顶点B、C分别在直线l2、l3上,若边BC与直线l3的夹角∠1=25°,则边AB与直线l1的夹角∠2=35°.
如图,直线l1∥l2∥l3,等边△ABC的顶点B、C分别在直线l2、l3上,若边BC与直线l3的夹角∠1=25°,则边AB与直线l1的夹角∠2=35°.