题目内容
9.计算:(1)$\sqrt{18}$-4$\sqrt{\frac{1}{2}}$+$\sqrt{24}$÷$\sqrt{3}$.
(2)-12016+($\frac{1}{2}$)-2-|4-$\sqrt{12}$|+(π-3)0-$\sqrt{27}$.
分析 (1)首先计算开方和乘法、除法,然后从左向右依次计算,求出算式的值是多少即可.
(2)首先计算乘方、开方,然后从左向右依次计算,求出算式的值是多少即可.
解答 解:(1)$\sqrt{18}$-4$\sqrt{\frac{1}{2}}$+$\sqrt{24}$÷$\sqrt{3}$
=3$\sqrt{2}$-4×$\frac{\sqrt{2}}{2}$+2$\sqrt{2}$
=3$\sqrt{2}$
(2)-12016+($\frac{1}{2}$)-2-|4-$\sqrt{12}$|+(π-3)0-$\sqrt{27}$
=-1+4-4+2$\sqrt{3}$+1-3$\sqrt{3}$
=-$\sqrt{3}$
点评 此题主要考查了二次根式的混合运算,要熟练掌握,解答此题的关键是要明确:①与有理数的混合运算一致,运算顺序先乘方再乘除,最后加减,有括号的先算括号里面的.②在运算中每个根式可以看做是一个“单项式”,多个不同类的二次根式的和可以看作“多项式”.

练习册系列答案
相关题目
9.甲、乙、丙三位运动员在相同条件下各射靶10次,每次射靶的成绩如下:
甲:9,10,8,5,7,8,10,8,8,7
乙:5,7,8,7,8,9,7,9,10,10
丙:7,6,8,5,4,7,6,3,9,5
(1)根据以上数据完成下表:
(2)根据表中数据分析,哪位运动员的成绩最稳定,并简要说明理由;
(3)比赛时三人依次出场,顺序由抽签方式决定,求甲、乙相邻出场的概率.
甲:9,10,8,5,7,8,10,8,8,7
乙:5,7,8,7,8,9,7,9,10,10
丙:7,6,8,5,4,7,6,3,9,5
(1)根据以上数据完成下表:
| 平均数 | 中位数 | 方差 | |
| 甲 | 8 | 8 | 2 |
| 乙 | 8 | 8 | 2.2 |
| 丙 | 6 | 6 | 3 |
(3)比赛时三人依次出场,顺序由抽签方式决定,求甲、乙相邻出场的概率.
19.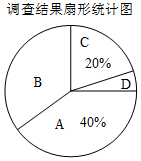 某课外活动小组为了解本校学生上学常用的一种交通方式,随机调查了本校部分学生,根据调查结果,统计整理并制作了如图尚不完整的统计图表:
某课外活动小组为了解本校学生上学常用的一种交通方式,随机调查了本校部分学生,根据调查结果,统计整理并制作了如图尚不完整的统计图表:
请根据以上信息解答下列问题:
(1)参与本次调查的学生共有160人;
(2)统计表中,m=56,n=32;扇形统计图中,B组所对应的圆心角的度数为126°;
(3)若该校共有1500名学生,请估计全校骑自行车上学的学生人数;
(4)该小组据此次调查结果向学校建议扩建学生车棚,若平均每4平方米能停放5辆自行车,请估计在现有300平方米车棚的基础上,至少还需要扩建多少平方米才能满足学生停车需求.
 某课外活动小组为了解本校学生上学常用的一种交通方式,随机调查了本校部分学生,根据调查结果,统计整理并制作了如图尚不完整的统计图表:
某课外活动小组为了解本校学生上学常用的一种交通方式,随机调查了本校部分学生,根据调查结果,统计整理并制作了如图尚不完整的统计图表:请根据以上信息解答下列问题:
| 组别 | 上学常用的一种交通方式 | 频数(人数) |
| A | 步行 | 64 |
| B | 骑自行车 | m |
| C | 乘公交车 | n |
| D | 其它 | 8 |
(2)统计表中,m=56,n=32;扇形统计图中,B组所对应的圆心角的度数为126°;
(3)若该校共有1500名学生,请估计全校骑自行车上学的学生人数;
(4)该小组据此次调查结果向学校建议扩建学生车棚,若平均每4平方米能停放5辆自行车,请估计在现有300平方米车棚的基础上,至少还需要扩建多少平方米才能满足学生停车需求.
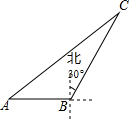 如图,海中一渔船在A处且与小岛C相距70nmile,若该渔船由西向东航行30nmile到达B处,此时测得小岛C位于B的北偏东30°方向上;求该渔船此时与小岛C之间的距离.
如图,海中一渔船在A处且与小岛C相距70nmile,若该渔船由西向东航行30nmile到达B处,此时测得小岛C位于B的北偏东30°方向上;求该渔船此时与小岛C之间的距离.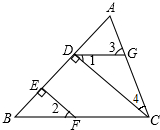 如图,CD⊥AB,EF⊥AB,∠1=∠2,∠ACB=70°,求∠3的度数.
如图,CD⊥AB,EF⊥AB,∠1=∠2,∠ACB=70°,求∠3的度数. 如图,已知:∠1=∠2,∠C=∠D,点B,E分别在线段AC,DF上.试说明∠A=∠F的理由.
如图,已知:∠1=∠2,∠C=∠D,点B,E分别在线段AC,DF上.试说明∠A=∠F的理由.