题目内容
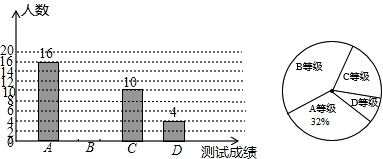
19. 某课外活动小组为了解本校学生上学常用的一种交通方式,随机调查了本校部分学生,根据调查结果,统计整理并制作了如图尚不完整的统计图表:
某课外活动小组为了解本校学生上学常用的一种交通方式,随机调查了本校部分学生,根据调查结果,统计整理并制作了如图尚不完整的统计图表:请根据以上信息解答下列问题:
| 组别 | 上学常用的一种交通方式 | 频数(人数) |
| A | 步行 | 64 |
| B | 骑自行车 | m |
| C | 乘公交车 | n |
| D | 其它 | 8 |
(2)统计表中,m=56,n=32;扇形统计图中,B组所对应的圆心角的度数为126°;
(3)若该校共有1500名学生,请估计全校骑自行车上学的学生人数;
(4)该小组据此次调查结果向学校建议扩建学生车棚,若平均每4平方米能停放5辆自行车,请估计在现有300平方米车棚的基础上,至少还需要扩建多少平方米才能满足学生停车需求.
分析 (1)根据题意即可得到结论;
(2)根据题意列式计算即可;
(3)根据题意列式计算即可;
(4)首先计算出现在的车棚面积-原有的车棚面积即可得到结论.
解答 解:(1)64÷40%=160人,
答:参与本次调查的学生共有160人;
故答案为:160;
(2)n=160×20%=32人,m=160-64-32-8=56,B组所对应的圆心角的度数=360°×$\frac{56}{160}$=126°,
故答案为:56,32,126°;
(3)全校骑自行车上学的学生人数约有1500×$\frac{56}{160}$=525(人);
(4)$\frac{525}{5}$×4-300=120(平方米)
∴至少还需要扩建120平方米,才能满足学生停车需求.
点评 本题考查的是条形统计图和扇形统计图的综合运用.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图中各部分占总体的百分比之和为1,直接反映部分占总体的百分比大小.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.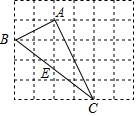 如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,若点E是BC的中点,则sin∠CAE的值为( )
如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,若点E是BC的中点,则sin∠CAE的值为( )
 如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,若点E是BC的中点,则sin∠CAE的值为( )
如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,若点E是BC的中点,则sin∠CAE的值为( )| A. | 2 | B. | $\frac{1}{2}$ | C. | $\sqrt{5}$ | D. | $\frac{{\sqrt{5}}}{5}$ |
7.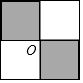 定义:用形状、大小完全相同的一种或几种平面图进行拼接,彼此之间不留空隙,不重叠地铺成一片,称为平面图形的镶嵌,如图是只选用大小相同的正方形在某顶点O周围拼接成的镶嵌图案.判断:若只选用一种大小相同的正多边形,在下列四个选项中,能进行平面镶嵌的是( )
定义:用形状、大小完全相同的一种或几种平面图进行拼接,彼此之间不留空隙,不重叠地铺成一片,称为平面图形的镶嵌,如图是只选用大小相同的正方形在某顶点O周围拼接成的镶嵌图案.判断:若只选用一种大小相同的正多边形,在下列四个选项中,能进行平面镶嵌的是( )
 定义:用形状、大小完全相同的一种或几种平面图进行拼接,彼此之间不留空隙,不重叠地铺成一片,称为平面图形的镶嵌,如图是只选用大小相同的正方形在某顶点O周围拼接成的镶嵌图案.判断:若只选用一种大小相同的正多边形,在下列四个选项中,能进行平面镶嵌的是( )
定义:用形状、大小完全相同的一种或几种平面图进行拼接,彼此之间不留空隙,不重叠地铺成一片,称为平面图形的镶嵌,如图是只选用大小相同的正方形在某顶点O周围拼接成的镶嵌图案.判断:若只选用一种大小相同的正多边形,在下列四个选项中,能进行平面镶嵌的是( )| A. | 正五角形 | B. | 正六边形 | C. | 正八边形 | D. | 正十边形 |
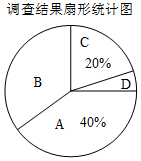
8.小明在学习了数据的收集、整理与描述后,为妈妈整理记录了10月份的家庭支出情况,并绘制成如下尚不完整的统计图表,请你根据图表信息完成下列各题:
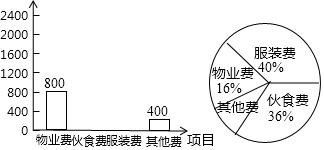
(1)10月份小明家共支出多少元?
(2)在扇形统计图中,表示“其他费”的扇形圆心角为多少度?
(3)请将表格补充完整;
(4)请将条形统计图补充完整.
| 项目 | 物业费 | 伙食费 | 服装费 | 其他费 |
| 金额/元 | 800 | 400 |

(1)10月份小明家共支出多少元?
(2)在扇形统计图中,表示“其他费”的扇形圆心角为多少度?
(3)请将表格补充完整;
(4)请将条形统计图补充完整.
9.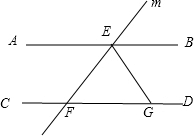 如图,已知直线AB∥CD,直线m与AB、CD相交于点E、F,EG平分∠FEB,∠EFG=50°,则∠FEG的度数为( )
如图,已知直线AB∥CD,直线m与AB、CD相交于点E、F,EG平分∠FEB,∠EFG=50°,则∠FEG的度数为( )
 如图,已知直线AB∥CD,直线m与AB、CD相交于点E、F,EG平分∠FEB,∠EFG=50°,则∠FEG的度数为( )
如图,已知直线AB∥CD,直线m与AB、CD相交于点E、F,EG平分∠FEB,∠EFG=50°,则∠FEG的度数为( )| A. | 65° | B. | 55° | C. | 45° | D. | 40° |
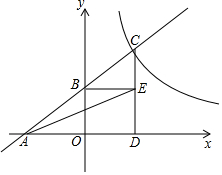 如图,直线AB与x轴交于点A,与y轴交于点B,与双曲线y=$\frac{k}{x}$(k>0)交于点C,过点C作CD⊥x轴于点D,过点B作BE⊥CD于点E,tan∠BCE=$\frac{3}{2}$,点E的坐标为(2,$\frac{3}{2}$),连接AE.
如图,直线AB与x轴交于点A,与y轴交于点B,与双曲线y=$\frac{k}{x}$(k>0)交于点C,过点C作CD⊥x轴于点D,过点B作BE⊥CD于点E,tan∠BCE=$\frac{3}{2}$,点E的坐标为(2,$\frac{3}{2}$),连接AE.