题目内容
13．解不等式组$\left\{\begin{array}{l}{3x-（x-2）≥6}\\{x+1＞\frac{4x-1}{3}}\end{array}\right.$．并写出它的整数解．分析 分别求出不等式组中两不等式的解集，找出两解集的公共部分确定出不等式组的解集，找出解集中的整数解即可．
解答 解：$\left\{\begin{array}{l}{3x-（x-2）≥6①}\\{x+1＞\frac{4x-1}{3}②}\end{array}\right.$
由①得：x≥2，
由②得：x＜4，
所以这个不等式组的解集为：2≤x＜4．
不等式组的整数为：2、3．
点评 此题考查了解一元一次不等式组，熟练掌握不等式组取解集的方法是解本题的关键．
练习册系列答案
相关题目
4．
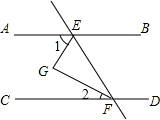如图，直线AB∥CD，EG，FG分别平分∠AEF和∠EFC，如果∠1=70°，那么∠2等于（ ）
如图，直线AB∥CD，EG，FG分别平分∠AEF和∠EFC，如果∠1=70°，那么∠2等于（ ）| A． | 40° | B． | 35° | C． | 25° | D． | 20° |
5．
如图，若AB是⊙O的直径，CD是⊙O的弦，∠ABD=58°，则∠BCD的度数为（ ）
如图，若AB是⊙O的直径，CD是⊙O的弦，∠ABD=58°，则∠BCD的度数为（ ）| A． | 32° | B． | 58° | C． | 64° | D． | 116° |