题目内容
12.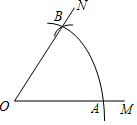 如图,以O为圆心,任意长为半径画弧,与射线OM交于点A,再以A为圆心,AO为半径画弧,两弧交于点B,画射线OB,则sin∠AOB的值等于$\frac{\sqrt{3}}{2}$.
如图,以O为圆心,任意长为半径画弧,与射线OM交于点A,再以A为圆心,AO为半径画弧,两弧交于点B,画射线OB,则sin∠AOB的值等于$\frac{\sqrt{3}}{2}$.
分析 连接AB,先根据题意判断出△AOB的形状,再得出∠AOB的度数,由特殊角的三角函数值即可得出结论.
解答  解:∵以O为圆心,任意长为半径画弧,与射线OM交于点A,
解:∵以O为圆心,任意长为半径画弧,与射线OM交于点A,
∴OA=OB,
∵以A为圆心,AO长为半径画弧,两弧交于点B,
∴△AOB是等边三角形,
∴∠AOB=60°,
∴sin∠AOB=sin60°=$\frac{\sqrt{3}}{2}$;
故答案为:$\frac{\sqrt{3}}{2}$.
点评 本题考查的是特殊角的三角函数值及等边三角形的判定与性质,熟记各特殊角的三角函数值是解答此题的关键.

练习册系列答案
相关题目
7.若二次函数的解析式为y=2x2-4x+3,则其函数图象与x轴交点的情况是( )
| A. | 没有交点 | B. | 有一个交点 | C. | 有两个交点 | D. | 以上都不对 |
1.-$\frac{1}{4}$的相反数是( )
| A. | 4 | B. | -$\frac{1}{4}$ | C. | $\frac{1}{4}$ | D. | -4 |
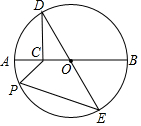 如图⊙O的半径为2,AB为直径.过AO的中点C作CD⊥AB交⊙O于点D,DE为⊙O的直径,点P为⊙O上动点,则2PC+PE的最小值是2$\sqrt{7}$.
如图⊙O的半径为2,AB为直径.过AO的中点C作CD⊥AB交⊙O于点D,DE为⊙O的直径,点P为⊙O上动点,则2PC+PE的最小值是2$\sqrt{7}$.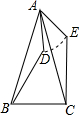 如图,在△ABC中,∠BAC=45°,AB=AC,D为△ABC内一点,AD=4,如果把△ABD绕点A按逆时针方向旋转,使AB与AC重合,求点D运动的路径长.
如图,在△ABC中,∠BAC=45°,AB=AC,D为△ABC内一点,AD=4,如果把△ABD绕点A按逆时针方向旋转,使AB与AC重合,求点D运动的路径长.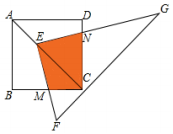 如图,点E在正方形ABCD的对角线AC上,且EC=2AE,直角三角形FEG的两直角边EF,EG分别交BC,DC于点M,N,若正方形ABCD的边长为a,则重叠部分四边形EMCN的面积为$\frac{4}{9}$a2.
如图,点E在正方形ABCD的对角线AC上,且EC=2AE,直角三角形FEG的两直角边EF,EG分别交BC,DC于点M,N,若正方形ABCD的边长为a,则重叠部分四边形EMCN的面积为$\frac{4}{9}$a2.