题目内容
2.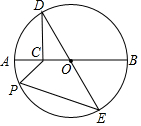 如图⊙O的半径为2,AB为直径.过AO的中点C作CD⊥AB交⊙O于点D,DE为⊙O的直径,点P为⊙O上动点,则2PC+PE的最小值是2$\sqrt{7}$.
如图⊙O的半径为2,AB为直径.过AO的中点C作CD⊥AB交⊙O于点D,DE为⊙O的直径,点P为⊙O上动点,则2PC+PE的最小值是2$\sqrt{7}$.
分析 延长OA到K,证明△COP∽△POK,根据相似三角形的对应边的比相等,即可证得PK=2PC,则2PC+PE的最小值就是KE的长,作EH⊥AB,在直角△KEH中利用勾股定理即可求得EK的长.
解答  解:延长OA到K,使AK=AO=2.
解:延长OA到K,使AK=AO=2.
∵O是AO的中点,
∴OC=$\frac{1}{2}$OA=1,
∴$\frac{OC}{OP}$=$\frac{OP}{OK}$=$\frac{1}{2}$.
又∵∠COP=∠POK,
∴△COP∽△POK,
∴$\frac{PC}{PK}$=$\frac{OC}{OP}$=$\frac{1}{2}$,即PK=2PC.
∴2PC+PE=PE+PK≥EK.
作EH⊥BC于点H.
∵在直角△COD中,cos∠DOC=$\frac{OC}{OD}$=$\frac{1}{2}$,
∴∠DOC=60°,
∴∠EOH=∠DOC=60°,
∴HE=OE•sin60°=2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$,
∴EK=$\sqrt{{5}^{2}+(\sqrt{3})^{2}}$=2$\sqrt{7}$.
即最小值是2$\sqrt{7}$.
故答案是:2$\sqrt{7}$.
点评 本题考查了相似三角形的判定与性质,以及路径最短问题,正确证明PK=2PC是解题的关键.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
12.下列式子去括号正确的是( )
| A. | -(2a-b)=-2a-b | B. | 3a+(4a2+2)=3a+4a2-2 | ||
| C. | -(2a+3y)=2a-3y | D. | -2(a-6)=-2a+12 |
13.已知,x,y,z为三个非负实数,且满足$\left\{\begin{array}{l}{3x+2y+z=5}\\{2x+y-3z=1}\end{array}\right.$,设S=3x+y-7z,则S的最大值是( )
| A. | -$\frac{1}{11}$ | B. | $\frac{1}{11}$ | C. | -$\frac{5}{7}$ | D. | -$\frac{7}{5}$ |
10.实数$\root{3}{27}$,0,-π,$\sqrt{16}$,$\sqrt{8}$,$\frac{1}{3}$,0.101 001 0001…(相邻两个1之间多一个0),其中无理数有( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
14.下列几何体中,属于棱柱的有( )


| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
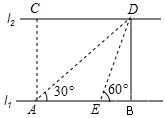 如图,河的两岸l1与l2相互平行,A、B是l1上的两点,C、D是l2上的两点,某人在点A处测得∠CAB=90°,∠DAB=30°,再沿AB方向前进60米到达点E(点E在线段AB上),测得∠DEB=60°,求河的宽度.
如图,河的两岸l1与l2相互平行,A、B是l1上的两点,C、D是l2上的两点,某人在点A处测得∠CAB=90°,∠DAB=30°,再沿AB方向前进60米到达点E(点E在线段AB上),测得∠DEB=60°,求河的宽度. 如图,在直角坐标系中以原点O为圆心的圆的半径由内向外依次Wie1,2,3,4,…,圆与直线y=x和y=-x分别交于:A2,A3,A4,…则点A80的坐标是(-4$\sqrt{2}$,4$\sqrt{2}$).
如图,在直角坐标系中以原点O为圆心的圆的半径由内向外依次Wie1,2,3,4,…,圆与直线y=x和y=-x分别交于:A2,A3,A4,…则点A80的坐标是(-4$\sqrt{2}$,4$\sqrt{2}$).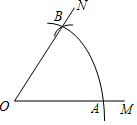 如图,以O为圆心,任意长为半径画弧,与射线OM交于点A,再以A为圆心,AO为半径画弧,两弧交于点B,画射线OB,则sin∠AOB的值等于$\frac{\sqrt{3}}{2}$.
如图,以O为圆心,任意长为半径画弧,与射线OM交于点A,再以A为圆心,AO为半径画弧,两弧交于点B,画射线OB,则sin∠AOB的值等于$\frac{\sqrt{3}}{2}$.