题目内容
19.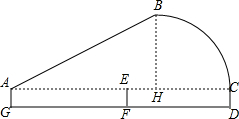 小明代表学校在邵阳市羽毛球比赛中,击出如图所示的球,其中A-B-C-D代表球飞行的弧度,经测量,小明同学击球时站在距离球网5m的G处,球网在点F处,而球落在球网对面的D处,DF=5m,击出球的角度约为30°,小明的击球高度约为1.6米,近似地把BC段看成$\frac{1}{4}$的圆,∠BHC=90°.比赛完后,小明想知道该球飞行的路程(即线段AB-C-D长)与球最高点B的高度,请你运用所学的知识帮他计算以下.($\sqrt{3}$≈1.73,π≈3.14,结果精确到0.1m)
小明代表学校在邵阳市羽毛球比赛中,击出如图所示的球,其中A-B-C-D代表球飞行的弧度,经测量,小明同学击球时站在距离球网5m的G处,球网在点F处,而球落在球网对面的D处,DF=5m,击出球的角度约为30°,小明的击球高度约为1.6米,近似地把BC段看成$\frac{1}{4}$的圆,∠BHC=90°.比赛完后,小明想知道该球飞行的路程(即线段AB-C-D长)与球最高点B的高度,请你运用所学的知识帮他计算以下.($\sqrt{3}$≈1.73,π≈3.14,结果精确到0.1m)
分析 设BH=HC=xm,在Rt△AHB中,根据$\frac{x}{10-x}$=tan30°,求出x的值、AB的值、$\widehat{BC}$的长,即可额求出飞行路线长;BH高度加上1.6米即为球的最高点.
解答 解:∵BC是$\frac{1}{4}$圆,
∴设BH=HC=xm,
则AH=(10-x)m,
在Rt△AHB中,$\frac{x}{10-x}$=tan30°,
解得x=5$\sqrt{3}$-5,
AB=2×(5$\sqrt{3}$-5)=(10$\sqrt{3}$-10)米,
$\widehat{BC}$的长为$\frac{1}{4}$×2π×(5$\sqrt{3}$-5)=($\frac{5\sqrt{3}}{2}$π-$\frac{5}{2}$)米,
∴飞行路线长为10$\sqrt{3}$-10+$\frac{5\sqrt{3}}{2}$π-$\frac{5}{2}$+1.6
=10×1.73-10+$\frac{5}{2}$×1.73×3.14-$\frac{5}{2}$+1.6
=17.3-10+2.5×1.73×3.14-2.5+1.6
=20.0米.
球最高点B的高度为1.6+BH=1.6+5$\sqrt{3}$-5=(5$\sqrt{3}$-3.4)米.
点评 本题考查了解直角三角形的应用,将飞行路线转化为三角形的边长和弧长是解题的关键.

练习册系列答案
相关题目
14.“鑫鑫”商店经销甲、乙两种商品,第一季度销售这两种商品共获利12000元,且1月,2月,3月的总利润比为8:7:9,甲、乙两种商品的成本与售价如表所示:
请根据以上信息,解答下列问题:
(1)1月份的总利润为4000元;
(2)已知2月份甲商品的销售量比1月份增加了10%,乙商品的销售价比1月份减少了20%,请分别求出1月份甲、乙两种商品的销售量;
(3)若3月份该商店销售乙商品的数量不超过甲商品数量的3倍,求3月份甲商品销售量的最小值.
| 商品 | 成本价(元/个) | 销售价(元/个) |
| 甲 | 20 | 40 |
| 乙 | 30 | 60 |
(1)1月份的总利润为4000元;
(2)已知2月份甲商品的销售量比1月份增加了10%,乙商品的销售价比1月份减少了20%,请分别求出1月份甲、乙两种商品的销售量;
(3)若3月份该商店销售乙商品的数量不超过甲商品数量的3倍,求3月份甲商品销售量的最小值.

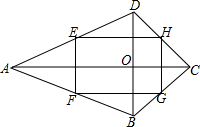 如图,在四边形ABCD中,AC⊥DB,垂足为O,点E、F、G、H分别为AD、AB、BC、CD的中点,求证:四边形EFGH是矩形.
如图,在四边形ABCD中,AC⊥DB,垂足为O,点E、F、G、H分别为AD、AB、BC、CD的中点,求证:四边形EFGH是矩形.