题目内容
9.抛物线y=-x2+(m-1)x+m与y轴交于点(0,3).(1)求抛物线的表达式;
(2)求抛物线的对称轴和顶点坐标;
(3)当x取什么值时,y的值随x的增大而减小?
分析 (1)把与y轴交于点(0,3)坐标代入即可求出m的值,即可求得解析式;
(2)把函数解析式配方化为顶点式即可求出抛物线的顶点坐标和对称轴方程;
(3)根据抛物线的性质即可判定.
解答 解:(1)∵抛物线y=-x2+(m-1)x+m与y轴交于点(0,3),
∴3=-02+(m-1)×0+m,
解得m=3
∴抛物线的解析式为y=-x2+2x+3,
(2)∵y=-x2+2x+3=-(x-1)2+4,
∴抛物线的顶点坐标为(1,4).
对称轴方程为x=1;
(3)∵a=-1<0,
∴当x>1时,y的值随x的增大而减小.
点评 本题考查了用代入法求函数解析式,抛物线的性质以及求二次函数的顶点坐标、对称方程等,熟练掌握抛物线的性质是解题的关键.

练习册系列答案
相关题目
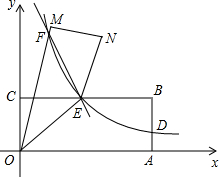 如图,矩形OABC在第一象限,OA=a,OC=b,双曲线y=$\frac{k}{x}$(x>0)始终经过BC的中点E,且与AB交于点D,连接OE.
如图,矩形OABC在第一象限,OA=a,OC=b,双曲线y=$\frac{k}{x}$(x>0)始终经过BC的中点E,且与AB交于点D,连接OE. 如图所示,在?ABCD中,AB=8,?ABCD的周长等于24,求其余三边的长.
如图所示,在?ABCD中,AB=8,?ABCD的周长等于24,求其余三边的长.
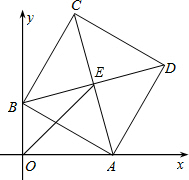 已知边长为a的正方形ABCD,两顶点A、B分别在平面直角坐标系的x轴、y轴的正半轴上滑动,点C点D在第一象限,点E为正方形ABCD的对称中心,连结OE,则OE的长的最大值是a.
已知边长为a的正方形ABCD,两顶点A、B分别在平面直角坐标系的x轴、y轴的正半轴上滑动,点C点D在第一象限,点E为正方形ABCD的对称中心,连结OE,则OE的长的最大值是a.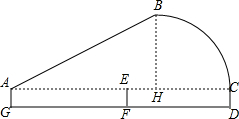 小明代表学校在邵阳市羽毛球比赛中,击出如图所示的球,其中A-B-C-D代表球飞行的弧度,经测量,小明同学击球时站在距离球网5m的G处,球网在点F处,而球落在球网对面的D处,DF=5m,击出球的角度约为30°,小明的击球高度约为1.6米,近似地把BC段看成$\frac{1}{4}$的圆,∠BHC=90°.比赛完后,小明想知道该球飞行的路程(即线段AB-C-D长)与球最高点B的高度,请你运用所学的知识帮他计算以下.($\sqrt{3}$≈1.73,π≈3.14,结果精确到0.1m)
小明代表学校在邵阳市羽毛球比赛中,击出如图所示的球,其中A-B-C-D代表球飞行的弧度,经测量,小明同学击球时站在距离球网5m的G处,球网在点F处,而球落在球网对面的D处,DF=5m,击出球的角度约为30°,小明的击球高度约为1.6米,近似地把BC段看成$\frac{1}{4}$的圆,∠BHC=90°.比赛完后,小明想知道该球飞行的路程(即线段AB-C-D长)与球最高点B的高度,请你运用所学的知识帮他计算以下.($\sqrt{3}$≈1.73,π≈3.14,结果精确到0.1m)