题目内容
14.“鑫鑫”商店经销甲、乙两种商品,第一季度销售这两种商品共获利12000元,且1月,2月,3月的总利润比为8:7:9,甲、乙两种商品的成本与售价如表所示:| 商品 | 成本价(元/个) | 销售价(元/个) |
| 甲 | 20 | 40 |
| 乙 | 30 | 60 |
(1)1月份的总利润为4000元;
(2)已知2月份甲商品的销售量比1月份增加了10%,乙商品的销售价比1月份减少了20%,请分别求出1月份甲、乙两种商品的销售量;
(3)若3月份该商店销售乙商品的数量不超过甲商品数量的3倍,求3月份甲商品销售量的最小值.
分析 (1)根据第一季度的总获利为12000元和三个月的利润比为8:7:9,可以求出1月份的利润;
(2)设1月份甲乙两种商品的销售量分别为x个、y个,根据1月份和2月份的获利情况,以及2月份甲商品的销售量比1月份增加了10%,乙商品的销售价比1月份减少了20%,可得关于x、y的二元一次方程组,解方程组即可;
(3)根据3月份的获利情况,得出关于a和b的不等式组,解不等式即可得出结论.
解答 解:(1)1月份的总利润为$12000×\frac{8}{8+7+9}=12000×\frac{1}{3}=4000$(元);
(2)2月份的总利润为$12000×\frac{7}{8+7+9}=1200×\frac{7}{24}=3500$(元),
设1月份甲乙两种商品的销售量分别为x个、y个,
根据题意列方程组得$\left\{\begin{array}{l}{20x+30y=4000}\\{20×(1+10%)x+[60×(1-20%)-30]y=3500}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=110}\\{y=60}\end{array}\right.$.
因此1月份甲、乙两种商品的销售量分别为110个、60个;
(3)3月份的销售利润为12000-4000-3500=4500(元),
设3月份甲乙两种商品的销售量分别为a个、b个,
则有$\left\{\begin{array}{l}{20a+30b=4500}\\{b≤3a}\end{array}\right.$,
所以$150-\frac{2}{3}a≤3a$,
解得$a≥\frac{450}{11}$.
因此3月份甲商品销售量的最小值为41个.
点评 本题主要考查的是二元一次方程组的应用和一元一次不等式组的应用,掌握应用二元一次方程组的应用和一元一次不等式组解决实际问题的方法是解题的关键.

| A. | $\frac{2\sqrt{3}}{3}$R,R,$\sqrt{3}$R2 | B. | R,$\frac{R}{2}$,2$\sqrt{3}$R2 | C. | $\frac{\sqrt{3}}{3}$R,R,2$\sqrt{3}$R2 | D. | R,$\frac{\sqrt{3}}{2}$R,$\frac{{3\sqrt{3}}}{2}{R^2}$ |
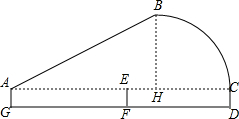 小明代表学校在邵阳市羽毛球比赛中,击出如图所示的球,其中A-B-C-D代表球飞行的弧度,经测量,小明同学击球时站在距离球网5m的G处,球网在点F处,而球落在球网对面的D处,DF=5m,击出球的角度约为30°,小明的击球高度约为1.6米,近似地把BC段看成$\frac{1}{4}$的圆,∠BHC=90°.比赛完后,小明想知道该球飞行的路程(即线段AB-C-D长)与球最高点B的高度,请你运用所学的知识帮他计算以下.($\sqrt{3}$≈1.73,π≈3.14,结果精确到0.1m)
小明代表学校在邵阳市羽毛球比赛中,击出如图所示的球,其中A-B-C-D代表球飞行的弧度,经测量,小明同学击球时站在距离球网5m的G处,球网在点F处,而球落在球网对面的D处,DF=5m,击出球的角度约为30°,小明的击球高度约为1.6米,近似地把BC段看成$\frac{1}{4}$的圆,∠BHC=90°.比赛完后,小明想知道该球飞行的路程(即线段AB-C-D长)与球最高点B的高度,请你运用所学的知识帮他计算以下.($\sqrt{3}$≈1.73,π≈3.14,结果精确到0.1m)