题目内容
10.某校欲举办“校园吉尼斯挑战赛”,为此该校在七年级中随机抽取一个班级进行了一次“你最喜欢的挑战项目”的问卷调查,已知被调查的班级的学生人数为50,根据收集到的数据,绘制成如下统计图表(不完整),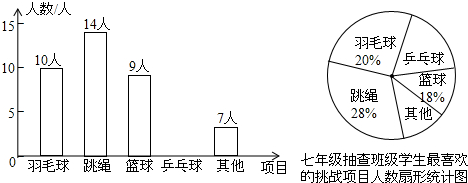
(1)问该班级中有多少同学喜欢乒乓球,并补充完整条形统计图;
(2)计算喜欢挑战“乒乓球”部分占总数的百分比;
(3)计算出“其他”项目所对应的圆心角度数;
(4)若全校学生约有3000人,请估计喜欢乒乓球和篮球的分别有多少人?
分析 (1)用总人数减去羽毛球、跳绳、篮球和其他的人数,求出喜欢乒乓球的人数,从而补全统计图;
(2)用喜欢挑战“乒乓球”的人数除以总人数即可得出答案;
(3)用360°乘以“其他”项目所占的百分比即可;
(4)用全校的总人数乘以喜欢乒乓球、篮球所占的百分比,即可求出喜欢乒乓球的人数和篮球的人数.
解答 解:(1)该班级喜欢乒乓球的同学有:50-10-14-9-7=10(人),
补图如下:
(2)喜欢挑战“乒乓球”部分占总数的百分比是$\frac{10}{50}$×100%=20%;
(3)“其他”项目所对应的圆心角度数是:360°×$\frac{7}{50}$=50.4°;
(4)喜欢乒乓球的人数是:3000×$\frac{10}{50}$=600(人);
喜欢蓝球的人数是:3000×18%=540(人);
点评 本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.

练习册系列答案
相关题目
2.正六边形半径为R,则它的边长、边心距、面积分别为( )
| A. | $\frac{2\sqrt{3}}{3}$R,R,$\sqrt{3}$R2 | B. | R,$\frac{R}{2}$,2$\sqrt{3}$R2 | C. | $\frac{\sqrt{3}}{3}$R,R,2$\sqrt{3}$R2 | D. | R,$\frac{\sqrt{3}}{2}$R,$\frac{{3\sqrt{3}}}{2}{R^2}$ |
 如图所示,在?ABCD中,AB=8,?ABCD的周长等于24,求其余三边的长.
如图所示,在?ABCD中,AB=8,?ABCD的周长等于24,求其余三边的长.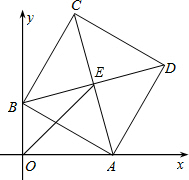 已知边长为a的正方形ABCD,两顶点A、B分别在平面直角坐标系的x轴、y轴的正半轴上滑动,点C点D在第一象限,点E为正方形ABCD的对称中心,连结OE,则OE的长的最大值是a.
已知边长为a的正方形ABCD,两顶点A、B分别在平面直角坐标系的x轴、y轴的正半轴上滑动,点C点D在第一象限,点E为正方形ABCD的对称中心,连结OE,则OE的长的最大值是a.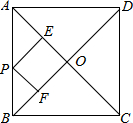 如图:正方形ABCD中,AC=10,P是AB上任意一点,PE⊥AC于E,PF⊥BD于F,则PE+PF=5.
如图:正方形ABCD中,AC=10,P是AB上任意一点,PE⊥AC于E,PF⊥BD于F,则PE+PF=5.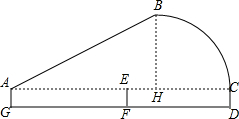 小明代表学校在邵阳市羽毛球比赛中,击出如图所示的球,其中A-B-C-D代表球飞行的弧度,经测量,小明同学击球时站在距离球网5m的G处,球网在点F处,而球落在球网对面的D处,DF=5m,击出球的角度约为30°,小明的击球高度约为1.6米,近似地把BC段看成$\frac{1}{4}$的圆,∠BHC=90°.比赛完后,小明想知道该球飞行的路程(即线段AB-C-D长)与球最高点B的高度,请你运用所学的知识帮他计算以下.($\sqrt{3}$≈1.73,π≈3.14,结果精确到0.1m)
小明代表学校在邵阳市羽毛球比赛中,击出如图所示的球,其中A-B-C-D代表球飞行的弧度,经测量,小明同学击球时站在距离球网5m的G处,球网在点F处,而球落在球网对面的D处,DF=5m,击出球的角度约为30°,小明的击球高度约为1.6米,近似地把BC段看成$\frac{1}{4}$的圆,∠BHC=90°.比赛完后,小明想知道该球飞行的路程(即线段AB-C-D长)与球最高点B的高度,请你运用所学的知识帮他计算以下.($\sqrt{3}$≈1.73,π≈3.14,结果精确到0.1m)