题目内容
3.(1)计算:$\sqrt{12}$-2cos30°+($\sqrt{3}$-1)0-($\frac{1}{8}$)-1(2)解不等式:$\frac{3-x}{2}$-(x-1)≤$\frac{5+x}{4}$,并把它的解集在数轴上表示出来.
分析 (1)分别按照0指数幂及负整数指数幂的计算法则、数的开方法则及特殊角的三角函数值计算出各数,再根据实数混合运算的法则进行计算即可;
(2)先去分母,再去括号,移项,合并同类项,把x的系数化为1,并在数轴上表示出来即可.
解答 解:(1)原式=2$\sqrt{3}$-2×$\frac{\sqrt{3}}{2}$+1-8
=2$\sqrt{3}$-$\sqrt{3}$+1-8
=$\sqrt{3}$-7;
(2)去分母得,2(3-x)-4(x-1)≤5+x,
去括号得,6-2x-4x+4≤5+x,
移项得,-2x-4x-x≤5-4-6,
合并同类项得,-7x≤-5,
把x的系数化为1得,x≥$\frac{5}{7}$.
在数轴上表示为: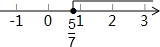 .
.
点评 本题考查的是解一元一次不等式,熟知解一元一次不等式的基本步骤是解答此题的关键.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
11.若抛物线y=ax2经过点P(1,-3),则此抛物线也经过点( )
| A. | (-1,3) | B. | (-3,1) | C. | (1,3) | D. | (-1,-3) |
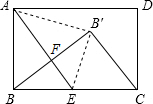 现有一张矩形纸片ABCD(如图),其中AB=4cm,BC=6cm,点E是BC的中点.实施操作:将纸片沿直线AE折叠,使点B落在矩形ABCD内,记为点B′.
现有一张矩形纸片ABCD(如图),其中AB=4cm,BC=6cm,点E是BC的中点.实施操作:将纸片沿直线AE折叠,使点B落在矩形ABCD内,记为点B′. 如图,已知:四边形ABCD是正方形,点E、F在对角线BD上,且BF=DE.
如图,已知:四边形ABCD是正方形,点E、F在对角线BD上,且BF=DE.