题目内容
20.$|\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}|$=ad-bc,例如$|\begin{array}{l}{2}&{3}\\{4}&{5}\end{array}|$=2×5×4=10-12=-2,再如$|\begin{array}{l}{x}&{2}\\{1}&{4}\end{array}|$=4x-2.按照这种运算的规定,请解答下列问题:(1)$|\begin{array}{l}{-1}&{2}\\{-2}&{0.5}\end{array}|$=3.5(只填写最后结果).
(2)当x=$\frac{1}{3}$时,$|\begin{array}{l}{x}&{\frac{1}{2}-x}\\{1}&{2}\end{array}|$=$\frac{1}{2}$.
分析 (1)原式利用题中的新定义计算即可得到结果;
(2)已知等式利用题中的新定义化简,求出解即可得到x的值.
解答 解:(1)根据题中的新定义得:原式=-0.5+4=3.5;
(2)已知等式利用题中的新定义化简得:2x-$\frac{1}{2}$+x=$\frac{1}{2}$,
解得:x=$\frac{1}{3}$.
故答案为:(1)3.5;(2)$\frac{1}{3}$.
点评 此题考查了解一元一次方程,以及有理数的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.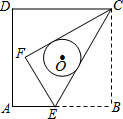 如图,正方形ABCD的边长为9,点E是AB上的一点,将△BCE沿CE折叠至△FCE,若CF,CE恰好与以正方形ABCD的中心为圆心的⊙O相切,则折痕CE的长为( )
如图,正方形ABCD的边长为9,点E是AB上的一点,将△BCE沿CE折叠至△FCE,若CF,CE恰好与以正方形ABCD的中心为圆心的⊙O相切,则折痕CE的长为( )
 如图,正方形ABCD的边长为9,点E是AB上的一点,将△BCE沿CE折叠至△FCE,若CF,CE恰好与以正方形ABCD的中心为圆心的⊙O相切,则折痕CE的长为( )
如图,正方形ABCD的边长为9,点E是AB上的一点,将△BCE沿CE折叠至△FCE,若CF,CE恰好与以正方形ABCD的中心为圆心的⊙O相切,则折痕CE的长为( )| A. | 4$\sqrt{3}$ | B. | $\frac{8}{3}$$\sqrt{3}$ | C. | 4$\sqrt{5}$ | D. | 6$\sqrt{3}$ |
 如图,正三角形A1B1C1的面积为1,取△A1B1C1各边的中点A2、B2、C2,作第二个正三角形A2B2C2,再取△A2B2C2各边的中点A3、B3、C3,作第三个正三角形A3B3C3,…,则第4个正三角形A4B4C4的面积是$\frac{1}{64}$;第n个正三角形AnBnCn的面积是$\frac{1}{{{4^{n-1}}}}$.
如图,正三角形A1B1C1的面积为1,取△A1B1C1各边的中点A2、B2、C2,作第二个正三角形A2B2C2,再取△A2B2C2各边的中点A3、B3、C3,作第三个正三角形A3B3C3,…,则第4个正三角形A4B4C4的面积是$\frac{1}{64}$;第n个正三角形AnBnCn的面积是$\frac{1}{{{4^{n-1}}}}$. 如图,AD=$\frac{2}{5}$BD,E是BC的中点,BE=2cm,AC=11cm,求线段DE的长.
如图,AD=$\frac{2}{5}$BD,E是BC的中点,BE=2cm,AC=11cm,求线段DE的长. 已知AE∥GF,BC∥GF,EF∥DC,EF∥AB,猜想∠A与∠C的关系如何?并说明理由.
已知AE∥GF,BC∥GF,EF∥DC,EF∥AB,猜想∠A与∠C的关系如何?并说明理由. 如图,∠A=∠D=90°,CD平分∠ACB,AB与CD相交于点E.
如图,∠A=∠D=90°,CD平分∠ACB,AB与CD相交于点E.