题目内容
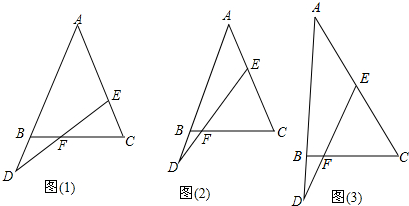
12.在等腰三角形ABC中,AB=AC,D是AB延长线上一点DE交BC于点F.(1)如图(1),若BD=CE,求证:DF=EF;
(2)如图(2),若BD=$\frac{1}{n}$CE,试写出DF和EF之间的数量关系
(3)如图(3),在(2)的条件下,若点E在CA的延长线上,那么(2)中的结论还成立吗?试说明.
分析 (1)作EG∥AB交BC于G,就可以得出∠EGC=∠ABC,∠DBF=∠EGF,∠D=∠GEF,就可以得出△DBF≌△EGF,就可以得出结论;
(2)图(2)过E作EG∥AB交BC于G,根据平行线的性质得到∠EGC=∠ABC,由等腰三角形的性质得到∠ABC=∠C,等量代换得到∠EGC=∠C,根据等腰三角形的判定得到EG=EC,通过△BDF∽△EFG,根据相似三角形的性质得到$\frac{BD}{EG}=\frac{DF}{EF}$,由于BD=$\frac{1}{n}$CE,即可得到$\frac{DF}{EF}=\frac{1}{n}$;
(3)方法同(2).
解答 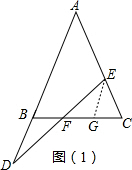 证明(1):如图(1)作EG∥AB交BC于G,
证明(1):如图(1)作EG∥AB交BC于G,
则∠CGE=∠ABC,∠GEF=∠D,∠DBF=∠EGF.
∵AB=AC,
∴∠ABC=∠C,
∴∠C=∠EGC,
∴CE=EG,
∵CE=BD,
∴BD=GE.
在△DBF和△EGF中,$\left\{\begin{array}{l}{∠D=∠GEF}\\{BD=GE}\\{∠DBF=∠EGF}\end{array}\right.$,
∴△DBF≌△EGF(ASA),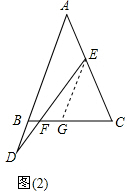
∴DF=EF;
(2)$\frac{DF}{EF}=\frac{1}{n}$,
理由:图(2)过E作EG∥AB交BC于G,
∴∠EGC=∠ABC,
∵AB=AC,
∴∠ABC=∠C,
∴∠EGC=∠C,
∴EG=EC,
∵EG∥AB,
∴△BDF∽△EFG,
∴$\frac{BD}{EG}=\frac{DF}{EF}$,
∵BD=$\frac{1}{n}$CE,
∴BD=$\frac{1}{n}$EG,
∴$\frac{DF}{EF}=\frac{1}{n}$;
(3)成立,如图(3),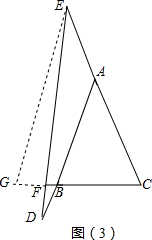
过E作EG∥AB交BC于G,
∴∠EGC=∠ABC,
∵AB=AC,
∴∠ABC=∠C,
∴∠EGC=∠C,
∴EG=EC,
∵EG∥AB,
∴△BDF∽△EFG,
∴$\frac{BD}{EG}=\frac{DF}{EF}$,
∵BD=$\frac{1}{n}$CE,
∴BD=$\frac{1}{n}$EG,
∴$\frac{DF}{EF}=\frac{1}{n}$.
点评 本题考查了相似三角形的判定和性质,等腰三角形的性质,平行线的性质,正确作出辅助线是解题的关键.

 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:①5a+b>0;
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:①5a+b>0;②a-b+c>0;③4a+2b+c<0;④(a+c)2<b2.其中,正确结论的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
| x | … | -1 | 0 | 1 | 2 | 3 | 4 | … |
| y | … | 0 | 3 | 4 | 3 | 0 | -5 | … |
(1)抛物线的对称轴是直线x=1;当x=-2时,对应的y值是-5;
(2)我们还发现,在对称轴右侧,当x每增加1个单位时,对应y值除了趋势逐渐变小外,在数量上还存在某种规律,试利用这一规律,直接写出当x=5时,对应的y值是-7;
(3)y≥-5时,x的取值范围是-2≤x≤4.
| A. | 4+5a=9a | B. | 6xy-x=6y | C. | 2x2+3x=5x3 | D. | 2a2b-2ba2=0 |