题目内容
5.若$\frac{{a}^{-1}+b}{a+{b}^{-1}}$=k,则$\frac{{a}^{-2}+{b}^{2}}{{a}^{2}+{b}^{-2}}$=( )| A. | k | B. | $\frac{1}{2}$k | C. | k2 | D. | $\frac{1}{2}$k2 |
分析 先根据题意得出$\frac{b}{a}$=k,再由负整数指数幂的运算法则把原式进行化简即可.
解答 解:∵$\frac{{a}^{-1}+b}{a+{b}^{-1}}$=$\frac{\frac{1}{a}+b}{a+\frac{1}{b}}$=$\frac{\frac{1+ab}{a}}{\frac{ab+1}{b}}$=$\frac{b}{a}$=k,
∴$\frac{{a}^{-2}+{b}^{2}}{{a}^{2}+{b}^{-2}}$=$\frac{\frac{1}{{a}^{2}}+{b}^{2}}{{a}^{2}+\frac{1}{{b}^{2}}}$=$\frac{\frac{1+{a}^{2}{b}^{2}}{{a}^{2}}}{\frac{{a}^{2}{b}^{2}+1}{{b}^{2}}}$=$\frac{{b}^{2}}{{a}^{2}}$=($\frac{b}{a}$)2=k2.
故选C.
点评 本题考查的是负整数指数幂,熟知非0数的负整数指数幂等于该数正整数指数幂的倒数是解答此题的关键.

练习册系列答案
相关题目
17.已知等腰三角形的底边长为10,腰长为13,则一腰上的高为( )
| A. | 12 | B. | $\frac{60}{13}$ | C. | $\frac{120}{13}$ | D. | $\frac{13}{5}$ |
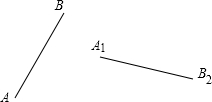 如图,线段AB绕点O顺时针旋转一定的角度得到线段A1B1(点A的对应点为A1).
如图,线段AB绕点O顺时针旋转一定的角度得到线段A1B1(点A的对应点为A1).
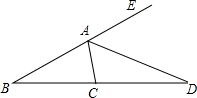 如图所示,AD平分∠CAE,∠B=30°,∠CAD=65°,则∠ACD=80°.
如图所示,AD平分∠CAE,∠B=30°,∠CAD=65°,则∠ACD=80°.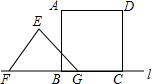 如图,正方形ABCD边长为8cm,FG是等腰直角△EFG的斜边,FG=10cm,点B、F、C、G都在直线l上,△EFG以1cm/s的速度沿直线l向右做匀速运动,当t=0时,点G与B重合,记t(0≤t≤8)秒时,正方形与三角形重合部分的面积是Scm2,则S与t之间的函数关系图象大致为( )
如图,正方形ABCD边长为8cm,FG是等腰直角△EFG的斜边,FG=10cm,点B、F、C、G都在直线l上,△EFG以1cm/s的速度沿直线l向右做匀速运动,当t=0时,点G与B重合,记t(0≤t≤8)秒时,正方形与三角形重合部分的面积是Scm2,则S与t之间的函数关系图象大致为( )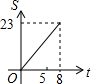
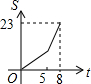
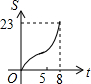
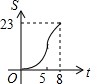
 数学老师在如图所示的黑板上写了一个关于x,y的方程,若$\left\{\begin{array}{l}{x=2}\\{y=-\frac{3}{2}}\end{array}\right.$和$\left\{\begin{array}{l}{x=\frac{1}{3}}\\{y=-4}\end{array}\right.$是该方程的两组解,则m,n的值分别为( )
数学老师在如图所示的黑板上写了一个关于x,y的方程,若$\left\{\begin{array}{l}{x=2}\\{y=-\frac{3}{2}}\end{array}\right.$和$\left\{\begin{array}{l}{x=\frac{1}{3}}\\{y=-4}\end{array}\right.$是该方程的两组解,则m,n的值分别为( )