题目内容
10．
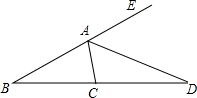如图所示，AD平分∠CAE，∠B=30°，∠CAD=65°，则∠ACD=80°．
分析 先根据角平分线求得∠DAE的度数，再根据∠DAE是△ABD的外角，求得∠D的度数，最后根据三角形内角和定理，求得∠ACD的度数．
解答 解：∵AD平分∠CAE，∠CAD=65°，
∴∠DAE=65°，
∵∠DAE是△ABD的外角，
∴∠D=∠DAE-∠B=65°-30°=35°，
∴△ACD中，∠ACD=180°-65°-35°=80°．
故答案为：80°
点评 本题主要考查了三角形的外角性质，解决问题的关键是掌握：三角形的一个外角等于和它不相邻的两个内角的和．
练习册系列答案
名师伴你成长课时同步学练测系列答案
相关题目
6．若三角形的两边长分别为6cm，9cm，则其第三边的长可能为（ ）
| A． | 2cm | B． | 3cm | C． | 7cm | D． | 16cm |
7．计算${（5\sqrt{5}）^2}$的结果是（ ）
| A． | 25 | B． | 125 | C． | $\sqrt{5}$ | D． | $25\sqrt{5}$ |
4．下列四对数值中是方程2x-y=1的解的是（ ）
| A． | $\left\{\begin{array}{l}{x=2}\\{y=0}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{x=-1}\\{y=-1}\end{array}\right.$ | C． | $\left\{\begin{array}{l}{x=0}\\{y=-1}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{x=-1}\\{y=1}\end{array}\right.$ |
5．若$\frac{{a}^{-1}+b}{a+{b}^{-1}}$=k，则$\frac{{a}^{-2}+{b}^{2}}{{a}^{2}+{b}^{-2}}$=（ ）
| A． | k | B． | $\frac{1}{2}$k | C． | k2 | D． | $\frac{1}{2}$k2 |
如图，已知直线AB、CD相交于点O，OE平分∠COB，若∠EOB=52°，则∠BOD等于76°．
2．甲、乙两人在100米直道AB上练习匀速往返跑，若甲、乙分别从A，B两端同时出发，分别到另一端点处掉头，掉头时间不计．甲、乙两人距A端的距离s（单位：m）与运动时间t（单位：s）之间的函数图象（0≤t≤200）如图所示．综合图象信息解答下列问题：
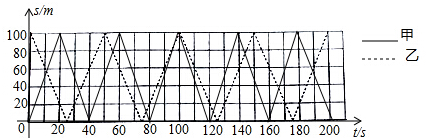
（1）求甲乙两人的速度；
（2）完成下列表格：
（3）在（2）的基础上，通过计算判断，当t=390s时，他们是否相遇？若相遇，应是第几次？并求出此时甲离A端的距离．
（1）求甲乙两人的速度；
（2）完成下列表格：
| 两人相遇次数（单位：次） | 1 | 2 | 3 | 4 | … | n |
| 两人所跑路程之和（单位：m） | 100 | 300 | 500 | 700 | … | 200n-100 |