题目内容
9.化简:(1)$\frac{1}{x-3}-\frac{6}{{x}^{2}-9}$
(2)$\frac{{x}^{2}-x}{{x}^{2}+2x+1}÷\frac{x-1}{x+1}$
(3)先化简,再求值:($\frac{1}{{a}^{2}-2a}-\frac{1}{{a}^{2}-4a+4}$)$÷\frac{2}{{a}^{2}-2a}$,其中a=5.
分析 (1)先通分,再把分子相加减即可;
(2)根据分式的除法法则进行计算即可;
(3)先根据分式混合运算的法则把原式进行化简,再把a的值代入进行计算即可.
解答 解:(1)原式=$\frac{x+3}{(x+3)(x-3)}$-$\frac{6}{(x+3)(x-3)}$
=$\frac{x+3-6}{(x+3)(x-3)}$
=$\frac{x-3}{(x+3)(x-3)}$
=$\frac{1}{x+3}$;
(2)原式=$\frac{x(x-1)}{(x+1)^{2}}$÷$\frac{x-1}{x+1}$
=$\frac{x(x-1)}{{(x+1)}^{2}}$•$\frac{x+1}{x-1}$
=$\frac{x}{x+1}$;
(3)原式=[$\frac{1}{a(a-2)}$-$\frac{1}{(a-2)^{2}}$]÷$\frac{2}{a(a-2)}$
=[$\frac{a-2}{{a(a-2)}^{2}}$-$\frac{a}{{(a-2)}^{2}}$]•$\frac{a(a-2)}{2}$
=$\frac{a-2-a}{{a(a-2)}^{2}}$•$\frac{a(a-2)}{2}$
=-$\frac{1}{a-2}$,
当a=5时,原式=-$\frac{1}{3}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
20.Rt△的三边a、b、c,则关于x的方程a(x2-1)-2cx+b(x2+1)=0的根的情况为( )
| A. | 有两个相等的实根 | B. | 有实根 | ||
| C. | 有两个不相等的实根 | D. | 没有实根 |
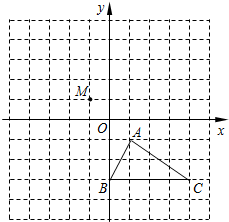 在如图所示的正方形网格中,△ABC的顶点均在格点上,建立平面直角坐标系后,点A的坐标为(1,-1).
在如图所示的正方形网格中,△ABC的顶点均在格点上,建立平面直角坐标系后,点A的坐标为(1,-1).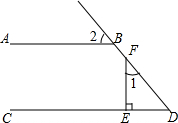 如图,AB∥CD,FE⊥CD,垂足为E,∠1=40°,则∠2的度数是50°.
如图,AB∥CD,FE⊥CD,垂足为E,∠1=40°,则∠2的度数是50°.