Question

14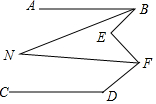．如图所示，AB∥CD，BN、FN分别平分∠ABE、∠EFD．已知∠BNF=α，∠BEF=β，∠FDC=γ，则下列等式中成立的是（　　）

• A． α+β+γ=180°
• B． -2α+β+γ=180°
• C． α+β+γ=360°
• D． -2α+β+γ=360°

Answer 1

分析 直接利用平行线的性质结合三角形内角和定理以及三角形外角的性质分析得出答案．

解答 解：如图所示：作EM∥AB，FK∥DC，延长FE交NB于点H，
∵EM∥AB，FK∥DC，AB∥CD，
∴∠ABE=∠BEM，∠MEF=∠EFK，∠KFD+∠CDF=180°，
∴∠ABE+∠EFK=∠BEM+∠MEF=β，∠KFD=180°-γ，
∴∠ABE+∠EFD=β+180°-γ，
∵BN、FN分别平分∠ABE、∠EFD，
∴∠NBE+∠NFE=$\frac{β+180°-γ}{2}$，
∵∠BNF+∠NFE=∠BHE，
∴∠BHE+∠HBE+∠HEB=∠BNF+∠EFN+∠HBE+∠BEH
=α+$\frac{β+180°-γ}{2}$+180°-β=180°，
∴整理得：-2α+β+γ=180°．
故选：B．

点评 此题主要考查了平行线的性质以及三角形内角和定理等知识，正确应用平行线的性质转化角的关系是解题关键．