题目内容
19．把抛物线y=x2先向左平移2个单位，再向上平移3个单位，平移后抛物线的表达式是y=（x+2）2+3．分析 只需看顶点坐标是如何平移得到的即可．
解答 解：原抛物线的顶点为（0，0），向左平移2个单位后再向上平移3个单位后，新顶点为（-2，3）．
即所得抛物线的顶点坐标是（-2，3）．
所以，平移后抛物线的表达式是y=（x+2）2+3，
故答案是：y=（x+2）2+3．
点评 考查了二次函数图象与几何变换，y=ax2（a≠0）的顶点坐标为（0，0）；抛物线的平移，看顶点的平移即可；上下平移，只改变顶点的纵坐标，上加下减．
练习册系列答案
相关题目
7．下列各组数中，把两数相乘，积为1的是（ ）
| A． | 2和-2 | B． | -2和$\frac{1}{2}$ | C． | $\sqrt{3}$和$\frac{\sqrt{3}}{3}$ | D． | $\sqrt{3}$和-$\sqrt{3}$ |
8．不等式组$\left\{\begin{array}{l}{2x+9≥3}\\{\frac{1+2x}{3}＞x-1}\end{array}\right.$的解集是（ ）
| A． | x≥-3 | B． | -3≤x＜4 | C． | -3≤x＜2 | D． | x＞4 |
海轮以每小时30nmile的速度航行，在点A处测得海上油井P在它的南偏东60°方向，向北航行40min后到达B处，测得油井P在南偏东30°方向，海轮改北偏东60在再航行120min到达C处，求P，C间的距离及此时点C在油井P的什么方向．
14．
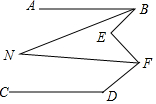如图所示，AB∥CD，BN、FN分别平分∠ABE、∠EFD．已知∠BNF=α，∠BEF=β，∠FDC=γ，则下列等式中成立的是（ ）
如图所示，AB∥CD，BN、FN分别平分∠ABE、∠EFD．已知∠BNF=α，∠BEF=β，∠FDC=γ，则下列等式中成立的是（ ）| A． | α+β+γ=180° | B． | -2α+β+γ=180° | C． | α+β+γ=360° | D． | -2α+β+γ=360° |