Question

20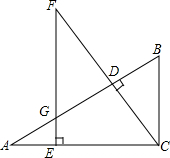．如图，在△ABC中，∠ACB=90°，CD⊥AB于点D，点E在AC上，CE=BC，过E点作AC的垂线，交CD的延长线于点F，EF交AB于G．求证：
（1）∠A=∠F；
（2）△ABC≌△FCE．

Answer 1

分析 （1）根据同角的余角相等可证∠A=∠F；
（2）根据AAS可证△ABC≌△FCE．

解答 证明：（1）∵EF⊥AC，
∴∠ACF+∠F=90°，
∵CD⊥AB，
∴∠ACF+∠A=90°，
∴∠A=∠F；
（2）在△ABC和△FCE中，
$\left\{\begin{array}{l}{∠A=∠F}\\{∠ACB=∠FEC=90°}\\{CE=BC}\end{array}\right.$，
∴△ABC≌△FCE（AAS）．

点评 本题主要考查了全等三角形的判定与性质，根据同角的余角相等证明∠A=∠F是解决问题的关键．