题目内容
已知⊙O的弦AC⊥BD于H，若半径为2，AH：DH=
，求DC．
| 3 |
考点：垂径定理,勾股定理
专题：计算题
分析：如图，连结AD、OC、OD，在Rt△DAH中，根据正切的定义可计算出∠DAH=30°，再根据圆周角定理得到∠COD=2∠DAH=60°，于是可判断△OCD为等边三角形，然后根据等边三角形的性质求解．
解答：解：如图，
连结AD、OC、OD，
∵AC⊥BD于H，
∴∠AHD=90°，
∵tan∠DAH=
，
而AH：DH=
，
∴tan∠DAH=
=
，
∴∠DAH=30°，
∴∠COD=2∠DAH=60°，
而OC=OD，
∴△OCD为等边三角形，
∴CD=OC=2．
连结AD、OC、OD，∵AC⊥BD于H，
∴∠AHD=90°，
∵tan∠DAH=
| DH |
| AH |
而AH：DH=
| 3 |
∴tan∠DAH=
| 1 | ||
|
| ||
| 3 |
∴∠DAH=30°，
∴∠COD=2∠DAH=60°，
而OC=OD，
∴△OCD为等边三角形，
∴CD=OC=2．
点评：本题考查了垂径定理：平分弦的直径平分这条弦，并且平分弦所对的两条弧．
练习册系列答案
全能测控期末小状元系列答案
相关题目
a，b，c三个数在数轴上的位置如图所示，则下列结论中错误的是（ ）| A、a+b＜0 |
| B、a+c＜0 |
| C、a-b＞0 |
| D、b-c＜0 |
如图，在正方形ABCD中，P、Q分别为BC、CD边上的点，且∠PAQ=45°，求证：PQ=PB+DQ．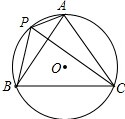
如图，A、P、B、C是⊙O上的四点，∠APC=∠CPB=60°．