题目内容
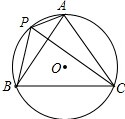 如图,A、P、B、C是⊙O上的四点,∠APC=∠CPB=60°.
如图,A、P、B、C是⊙O上的四点,∠APC=∠CPB=60°.(1)判断△ABC的形状并证明你的结论;
(2)过点A作AD⊥PC于点D,求证:PB+PD=CD.
考点:圆周角定理,全等三角形的判定与性质,等边三角形的判定与性质
专题:
分析:(1)利用圆周角定理可得∠BAC=∠CPB,∠ABC=∠APC,而∠APC=∠CPB=60°,所以∠BAC=∠ABC=60°,从而可判断△ABC的形状;
(2)在线段CD上截取DP′=DP,由全等三角形的判定定理可得出△AP′C≌△APB,由此可得出结论.
(2)在线段CD上截取DP′=DP,由全等三角形的判定定理可得出△AP′C≌△APB,由此可得出结论.
解答: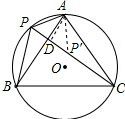 (1)解:△ABC是等边三角形.
(1)解:△ABC是等边三角形.
证明如下:在⊙O中
∵∠BAC与∠CPB是
所对的圆周角,∠ABC与∠APC是
所对的圆周角,
∴∠BAC=∠CPB,∠ABC=∠APC,
又∵∠APC=∠CPB=60°,
∴∠ABC=∠BAC=60°,
∴△ABC为等边三角形;
(2)证明:在线段CD上截取DP′=DP,
∵∠APC=60°,AD是PP′的垂直平分线,
∴AP=AP′,
∴△APP′是等边三角形,
∵∠BAC=60°,
∴∠PAB=∠P′AC.
在△AP′C与△APB中,
∵
,
∴△AP′C≌△APB,
∴PB=CP′,
∴PB+PD=CP′+CP′=CD.
 (1)解:△ABC是等边三角形.
(1)解:△ABC是等边三角形.证明如下:在⊙O中
∵∠BAC与∠CPB是
 |
| BC |
 |
| AC |
∴∠BAC=∠CPB,∠ABC=∠APC,
又∵∠APC=∠CPB=60°,
∴∠ABC=∠BAC=60°,
∴△ABC为等边三角形;
(2)证明:在线段CD上截取DP′=DP,
∵∠APC=60°,AD是PP′的垂直平分线,
∴AP=AP′,
∴△APP′是等边三角形,
∵∠BAC=60°,
∴∠PAB=∠P′AC.
在△AP′C与△APB中,
∵
|
∴△AP′C≌△APB,
∴PB=CP′,
∴PB+PD=CP′+CP′=CD.
点评:本题考查的是圆周角定理,熟知在同圆或等圆中,同弧或等弧所对的圆周角相等是解答此题的关键.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案
相关题目
 如图,在△ABC中,AB=AC,D是AB上一点.通过度量AB、DC、DB的长度,确定AB与
如图,在△ABC中,AB=AC,D是AB上一点.通过度量AB、DC、DB的长度,确定AB与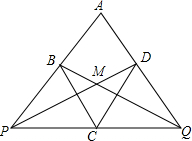 如图,菱形ABCD中,∠A=60°,过顶点C任意作一直线分别交AB、AD的延长线于P、Q两点,设PD、QB相交于点M.求证:∠PMQ=120°.
如图,菱形ABCD中,∠A=60°,过顶点C任意作一直线分别交AB、AD的延长线于P、Q两点,设PD、QB相交于点M.求证:∠PMQ=120°. 如图,在△ABC与△DEF中,AB=DE,∠B=∠E,AC=DF,判断△ABC与△DEF是否全等,并说明理由.
如图,在△ABC与△DEF中,AB=DE,∠B=∠E,AC=DF,判断△ABC与△DEF是否全等,并说明理由.