Question

在△ABC中，∠B=30°，AB=AC，AB的垂直平分线交AC所在的直线于P，交BC于Q，则∠CPQ=

 

．

Answer 1

考点：线段垂直平分线的性质,等腰三角形的性质

专题：

分析：由垂直平分线的定义可求得∠BQP=60°，由条件可得∠C=∠B=30°，再结合外角的性质可求得∠CPQ．

解答：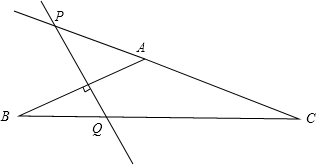
解：
∵PQ垂直平分AB，
∴∠B+∠PQB=90°，
∵∠B=30°，
∴∠PQB=90°-30°=60°，
∵AB=AC，
∴∠C=∠B=30°，
∵∠PQB是△PQC的一个外角，
∴∠PQB=∠C+∠CPQ，
∴∠CPQ=∠PQB-∠C=60°-30°=30°，
故答案为：30°．

点评：本题主要考查垂直平分线的定义及等腰三角形的性质，利用外角得到∠PQB=∠C+∠CPQ是解题的关键．