题目内容
已知线段OP=1,取OP的中点P1,取PP1的中点P2.
(1)比较线段OPn与OPn-1的大小(n为大于1的整数).
(2)若OP=1m,则n从何值开始,线段Pn-1Pn<1mm.
(1)比较线段OPn与OPn-1的大小(n为大于1的整数).
(2)若OP=1m,则n从何值开始,线段Pn-1Pn<1mm.
考点:比较线段的长短
专题:
分析:(1)利用已知线段长度结合图象进而分析比较线段长度即可;
(2)利用有理数的乘方运算法则进而得出n的值.
(2)利用有理数的乘方运算法则进而得出n的值.
解答: 解:(1)∵线段OP=1,取OP的中点P1,取PP1的中点P2,
解:(1)∵线段OP=1,取OP的中点P1,取PP1的中点P2,
∴OP1=
,P1P2=
,P2P3=
,P3P4=
,
如图所示:当n为偶数时,OPn>OPn-1,
当n为奇数时,OPn<OPn-1;
(2)∵OP=1,则OP1=
,P1P2=
=(
)2,P2P3=
=(
)3,P3P4=
=(
)4,
∴Pn-1Pn=(
)n,
∵OP=1m=1000mm,
∵1000×(
)n<1,
当n=10,(
)n=
,
故n≥10时,线段Pn-1Pn<1mm.
 解:(1)∵线段OP=1,取OP的中点P1,取PP1的中点P2,
解:(1)∵线段OP=1,取OP的中点P1,取PP1的中点P2,∴OP1=
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 16 |
如图所示:当n为偶数时,OPn>OPn-1,
当n为奇数时,OPn<OPn-1;
(2)∵OP=1,则OP1=
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 8 |
| 1 |
| 2 |
| 1 |
| 16 |
| 1 |
| 2 |
∴Pn-1Pn=(
| 1 |
| 2 |
∵OP=1m=1000mm,
∵1000×(
| 1 |
| 2 |
当n=10,(
| 1 |
| 2 |
| 1 |
| 1024 |
故n≥10时,线段Pn-1Pn<1mm.
点评:此题主要考查了比较线段长度,利用数形结合得出是解题关键.

练习册系列答案
相关题目
数轴上的两点M、N分别表示5和-2,那么M、N两点间的距离是( )
| A、5+(-2) |
| B、(-2)-5 |
| C、|5-(-2)| |
| D、-2-5 |
 如图,在?ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点,连接AG、BH、CE、DF相交于I、J、K、L,若?ABCD的面积为1,求四边形IJKL的面积.
如图,在?ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点,连接AG、BH、CE、DF相交于I、J、K、L,若?ABCD的面积为1,求四边形IJKL的面积.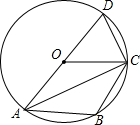 如图,四边形ABCD的四个顶点都在⊙O上,圆心O在AD上,OC∥AB.
如图,四边形ABCD的四个顶点都在⊙O上,圆心O在AD上,OC∥AB.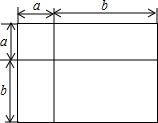 如图,你能根据图形推导出一个什么样的结论?
如图,你能根据图形推导出一个什么样的结论?