题目内容
5.(1)分解因式:①-x3+6x2-9x;②(2a+b)2-(a+2b)2(2)计算:($\frac{x+8}{{x}^{2}-4}$-$\frac{2}{x-2}$)÷$\frac{x-4}{{x}^{2}-4x+4}$
(3)已知$\frac{x}{y}$=-2,求$\frac{x}{x-y}$-$\frac{y}{x+y}$-$\frac{{y}^{2}}{{x}^{2}-{y}^{2}}$的值.
分析 (1)①先提取-x,再根据完全平方公式进行因式分解,即可得出答案;
②根据平方差公式进行计算即可;
(2)先把分母进行通分,再把除法转化成乘法,然后约分即可;
(3)先把分式转成化成同分母,再根据分式的加法运算法则进行计算,然后约分即可得出答案.
解答 解:(1)①原式=-x(x2-6x+9)=-x(x-3)2;
②原式=(2a+b+a+2b)(2a+b-a-2b)=3(a+b)(a-b);
(2)解:原式=$\frac{x+8-2(x+2)}{(x+2)(x-2)}$•$\frac{(x-2)^{2}}{x-4}$=$\frac{-(x-4)}{(x+2)(x-2)}$•$\frac{(x-2)^{2}}{x-4}$=-$\frac{x-2}{x+2}$;
(3)解:原式=$\frac{x(x+y)-y(x-y)-{y}^{2}}{(x-y)(x+y)}$=$\frac{{x}^{2}+xy-xy+{y}^{2}-{y}^{2}}{(x-y)(x+y)}$=$\frac{{x}^{2}}{{x}^{2}-{y}^{2}}$,
因为$\frac{x}{y}$=-2,所以x=-2y,所以原式=$\frac{4{y}^{2}}{3{y}^{2}}$=$\frac{4}{3}$.
点评 此题考查了分式的化简求值和提公因式法与公式法的综合运用,熟练掌握运算公式是解题的关键.

练习册系列答案
相关题目
16. 如图,某厂生产一种扇形折扇,OB=10cm,AB=20cm,其中裱花的部分是用纸糊的,若扇子完全打开摊平时纸面面积为$\frac{1000}{3}$π cm2,则扇形圆心角的度数为( )
如图,某厂生产一种扇形折扇,OB=10cm,AB=20cm,其中裱花的部分是用纸糊的,若扇子完全打开摊平时纸面面积为$\frac{1000}{3}$π cm2,则扇形圆心角的度数为( )
 如图,某厂生产一种扇形折扇,OB=10cm,AB=20cm,其中裱花的部分是用纸糊的,若扇子完全打开摊平时纸面面积为$\frac{1000}{3}$π cm2,则扇形圆心角的度数为( )
如图,某厂生产一种扇形折扇,OB=10cm,AB=20cm,其中裱花的部分是用纸糊的,若扇子完全打开摊平时纸面面积为$\frac{1000}{3}$π cm2,则扇形圆心角的度数为( )| A. | 120° | B. | 140° | C. | 150° | D. | 160° |
17.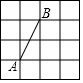 如图4×4的正方形网格中,网格线的交点叫格点,已知点A、B是格点,若C也是格点且△ABC为等腰三角形,则点C的个数是( )
如图4×4的正方形网格中,网格线的交点叫格点,已知点A、B是格点,若C也是格点且△ABC为等腰三角形,则点C的个数是( )
 如图4×4的正方形网格中,网格线的交点叫格点,已知点A、B是格点,若C也是格点且△ABC为等腰三角形,则点C的个数是( )
如图4×4的正方形网格中,网格线的交点叫格点,已知点A、B是格点,若C也是格点且△ABC为等腰三角形,则点C的个数是( )| A. | 6个 | B. | 7个 | C. | 8个 | D. | 9个 |
 如图,在矩形ABCD中,AB=2,BC=1.动点P从点B出发,沿路线B-C-D作匀速运动.那么△ABP的面积S与点P的运动路程x之间的函数图象大致是( )
如图,在矩形ABCD中,AB=2,BC=1.动点P从点B出发,沿路线B-C-D作匀速运动.那么△ABP的面积S与点P的运动路程x之间的函数图象大致是( )



 如图是一块长、宽、高分别为4cm、2cm和1cm的长方体木块,一只蚂蚁要从长方体木块的-个顶点A处,沿着长方体木块的表面爬到长方体木块上和顶点A相对的顶点B处吃食物,那么它需要爬行的最短路径的长是5cm.
如图是一块长、宽、高分别为4cm、2cm和1cm的长方体木块,一只蚂蚁要从长方体木块的-个顶点A处,沿着长方体木块的表面爬到长方体木块上和顶点A相对的顶点B处吃食物,那么它需要爬行的最短路径的长是5cm. 有理数a、b在数轴上的对应的位置如图所示,则下列各式①a+b<0;②a-b>0;③ab>0;④|a|>b;⑤1-b>0;⑥a+1>0,一定成立的有( )
有理数a、b在数轴上的对应的位置如图所示,则下列各式①a+b<0;②a-b>0;③ab>0;④|a|>b;⑤1-b>0;⑥a+1>0,一定成立的有( )