题目内容
15. 某度假村依山而建,大门A处,有一斜坡AB,长度为13米,在坡顶B处测得度假村楼CF的楼顶C的仰角∠CBF=60?,离B点8米远的E处有一花台,在E处仰望C的仰角∠CEF=73.5°,CF的延长线交校门处的水平面于D点,FD=5米.
某度假村依山而建,大门A处,有一斜坡AB,长度为13米,在坡顶B处测得度假村楼CF的楼顶C的仰角∠CBF=60?,离B点8米远的E处有一花台,在E处仰望C的仰角∠CEF=73.5°,CF的延长线交校门处的水平面于D点,FD=5米.(1)求斜坡AB的坡度i.
(2)求DC的长.(参考数据:sin73.5°≈0.96,con73.5°≈0.28,tan73.5°≈3.4,$\sqrt{3}$≈1.7)
分析 (1)过B作BG⊥AD于G,则四边形BGDF是矩形,求得BG=DF=5米,然后根据勾股定理求得AG,即可求得斜坡AB的坡度i;
(2)在Rt△BCF中,BF=$\frac{CF}{tan∠CBF}$=$\frac{CF}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$CF,在Rt△CEF中,EF=$\frac{CF}{tan∠CEF}$=$\frac{CF}{3.4}$=$\frac{5}{17}$CF,根据BF-EF=8得出方程$\frac{\sqrt{3}}{3}$CF-$\frac{5}{17}$CF=8,解方程求出CF,进而求得.
解答  解:(1)过B作BG⊥AD于G,
解:(1)过B作BG⊥AD于G,
则四边形BGDF是矩形,
∴BG=DF=5米,
∵AB=13米,
∴AG=$\sqrt{1{3}^{2}-{5}^{2}}$=12米,
∴AB的坡度i=$\frac{BG}{AG}$=$\frac{5}{12}$=1:2.4;
(2)在Rt△BCF中,BF=$\frac{CF}{tan∠CBF}$=$\frac{CF}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$CF,
在Rt△CEF中,EF=$\frac{CF}{tan∠CEF}$=$\frac{CF}{3.4}$=$\frac{5}{17}$CF,
∵BF-EF=BE=8米,
∴$\frac{\sqrt{3}}{3}$CF-$\frac{5}{17}$CF=8,
解得:CF≈29.35.
∴DC=CF+DF≈29.35+5≈34.4米.
点评 本题考查了解直角三角形的应用-仰角和俯角问题,解直角三角形的应用-坡度和坡比问题,勾股定理,能够正确作出辅助线构造直角三角形并解直角三角形是解题的关键.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
8.下列图形中是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
10.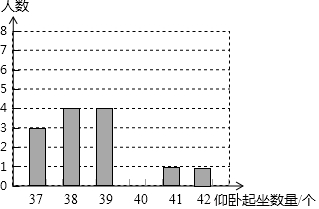 某校为了解本校九年级女生“仰卧起坐”的训练情况,随机抽查了该年级m名女生进行测试,并按测试成绩绘制出以下两幅不完整的统计表,请根据图中的信息解答下列问题
某校为了解本校九年级女生“仰卧起坐”的训练情况,随机抽查了该年级m名女生进行测试,并按测试成绩绘制出以下两幅不完整的统计表,请根据图中的信息解答下列问题
(1)m=20p=15
(2)补全上面的条形统计图;
(3)被抽取的女生“仰卧起坐”测试成绩的众数是40;
(4)若该年级有320名女生,请你估计该年级女生中“仰卧起坐”测试成绩为37的人数.
 某校为了解本校九年级女生“仰卧起坐”的训练情况,随机抽查了该年级m名女生进行测试,并按测试成绩绘制出以下两幅不完整的统计表,请根据图中的信息解答下列问题
某校为了解本校九年级女生“仰卧起坐”的训练情况,随机抽查了该年级m名女生进行测试,并按测试成绩绘制出以下两幅不完整的统计表,请根据图中的信息解答下列问题| 测试成绩(个) | 学生数(名) | 百分比 |
| 37 | 3 | P% |
| 38 | 4 | 20% |
| 39 | 4 | 20% |
| 40 | N | 35% |
| 41 | 1 | 5% |
| 42 | 1 | 5% |
(2)补全上面的条形统计图;
(3)被抽取的女生“仰卧起坐”测试成绩的众数是40;
(4)若该年级有320名女生,请你估计该年级女生中“仰卧起坐”测试成绩为37的人数.
7.我市某一周的日最高气温统计如下表:
则这周日最高气温的中位数是27℃.
| 最高气温(℃) | 25 | 26 | 27 | 28 |
| 天数(天) | 1 | 1 | 2 | 3 |
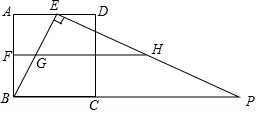 如图,正方形ABCD的边长为4,点E、F分别是边AD、AB的中点,点P是BC延长线上一点,且EP⊥EB,过点F作FH∥BP,分别交EB、EP于G、H两点,将△EGH绕点E逆时针旋转α(0°<α<90°),得到△EMN(M、N分别是G、H的对应点),使直线MN恰好经过点B.
如图,正方形ABCD的边长为4,点E、F分别是边AD、AB的中点,点P是BC延长线上一点,且EP⊥EB,过点F作FH∥BP,分别交EB、EP于G、H两点,将△EGH绕点E逆时针旋转α(0°<α<90°),得到△EMN(M、N分别是G、H的对应点),使直线MN恰好经过点B.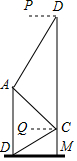 如图,某中学在教学楼前新建了一座雕塑AB,为了测量雕塑的高度,小明在二楼找到一点C,利用三角尺测得雕塑顶端点A的仰角∠QCA为45°,底部点B的俯角∠QCB为30°,小华在五楼找到一点D,利用三角尺测得点A的俯角∠PDA为60°,若AD为8m,则雕塑AB的高度为多少?(结果精确到0.1m,参考数据:$\sqrt{3}$≈1.73).
如图,某中学在教学楼前新建了一座雕塑AB,为了测量雕塑的高度,小明在二楼找到一点C,利用三角尺测得雕塑顶端点A的仰角∠QCA为45°,底部点B的俯角∠QCB为30°,小华在五楼找到一点D,利用三角尺测得点A的俯角∠PDA为60°,若AD为8m,则雕塑AB的高度为多少?(结果精确到0.1m,参考数据:$\sqrt{3}$≈1.73).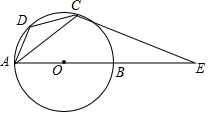 如图,AB为⊙O的直径,AD为弦,过⊙O上一点C作⊙O的切线交AB的延长线于E,且∠DCA=∠E.
如图,AB为⊙O的直径,AD为弦,过⊙O上一点C作⊙O的切线交AB的延长线于E,且∠DCA=∠E.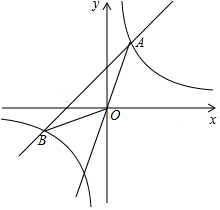 如图,直线y=4x与反比例函数y=$\frac{k}{x}$(k≠0)相交与点A(1,a),B是反比例函数图象上一点,直线OB与x轴的夹角为α,且tanα=$\frac{1}{4}$.
如图,直线y=4x与反比例函数y=$\frac{k}{x}$(k≠0)相交与点A(1,a),B是反比例函数图象上一点,直线OB与x轴的夹角为α,且tanα=$\frac{1}{4}$.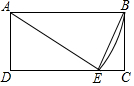 如图,矩形ABCD中,AB=10,AD=6,以A为圆心,AB为半径作圆弧交CD于E,连结EA,EB.则tan∠AEB的值为3.
如图,矩形ABCD中,AB=10,AD=6,以A为圆心,AB为半径作圆弧交CD于E,连结EA,EB.则tan∠AEB的值为3.