题目内容
4.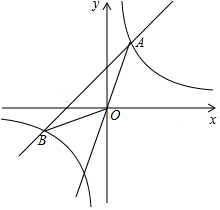 如图,直线y=4x与反比例函数y=$\frac{k}{x}$(k≠0)相交与点A(1,a),B是反比例函数图象上一点,直线OB与x轴的夹角为α,且tanα=$\frac{1}{4}$.
如图,直线y=4x与反比例函数y=$\frac{k}{x}$(k≠0)相交与点A(1,a),B是反比例函数图象上一点,直线OB与x轴的夹角为α,且tanα=$\frac{1}{4}$.(1)求k的值.
(2)求点B的坐标.
(3)设点P点在y轴上,若△PAB是以AB为直角边的直角三角形,则点P的坐标为:(0,5)或(0,-5).
分析 (1)根据直线y=4x经过点A(1,a),可得a的值,再将A的坐标代入反比例函数解析式,进而得到k的值;
(2)过点B作BE垂直于x轴于点E,设BE长为m,得出点B坐标为(-m,-4m),把点B代入$y=\frac{4}{x}$中,即可得到m的值;
(3)分两种情况:点P在y轴正半轴和负半轴上,分别根据AB⊥BP或AB⊥AP',以及点A,B的坐标,即可得到点P的坐标.
解答 解:(1)把点A(1,a)代入y=4x中,得a=4,
所以A(1,4),
把点A(1,4)代入$y=\frac{k}{x}$中,得k=4;
(2)过点B作BE垂直于x轴于点E,如图示,
设BE长为m,在Rt△OBE中,
∵$tanα=\frac{1}{4}$,
∴$\frac{BE}{OE}=\frac{1}{4}$,即 OE=4BE=4m,
∴所以点B坐标为(-m,-4m),
把点B代入$y=\frac{4}{x}$中,
得:4m2=4,
解得m1=1,m2=-1(舍去)
∴点B坐标为(-4,-1);
(3)如图所示,过A作AP'⊥AB,交y轴于P',过B作BP⊥AB,交y轴于P,
根据A(1,4),B(-4,-1),可得直线AB的解析式为y=x+3;
根据直角坐标系中互相垂直的两直线的系数k互为负倒数,
可设直线BP为y=-x+m,
把B(-4,-1)代入可得,m=-5;
设直线AP'的解析式为y=-x+n,
把A(1,4)代入,可得n=5,
∴点P坐标为:(0,5),(0,-5).
故答案为:(0,5)或(0,-5).
点评 本题主要考查了反比例函数与一次函数交点问题以及解直角三角形的运用,解决问题的关键是作辅助线构造直角三角形.解题时注意:直角坐标系中互相垂直的两直线的系数k互为负倒数.

练习册系列答案
相关题目
17.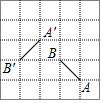 如图,在正方形网格中,线段A′B′是线段AB绕某点逆时针旋转角α得到的,点A′与A对应,则角α的大小为( )
如图,在正方形网格中,线段A′B′是线段AB绕某点逆时针旋转角α得到的,点A′与A对应,则角α的大小为( )
 如图,在正方形网格中,线段A′B′是线段AB绕某点逆时针旋转角α得到的,点A′与A对应,则角α的大小为( )
如图,在正方形网格中,线段A′B′是线段AB绕某点逆时针旋转角α得到的,点A′与A对应,则角α的大小为( )| A. | 30° | B. | 60° | C. | 90° | D. | 120° |
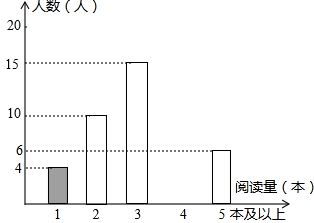
13.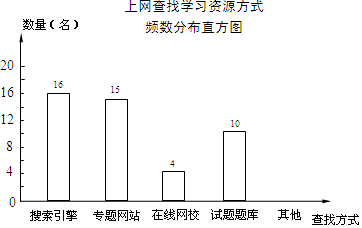 某学校为了了解本校学生采用何种方式上网查找所需要的学习资源,随机抽取部分学生了解情况,并将统计结果绘制成频数分布表及频数分布直方图.
某学校为了了解本校学生采用何种方式上网查找所需要的学习资源,随机抽取部分学生了解情况,并将统计结果绘制成频数分布表及频数分布直方图.
上网查找学习资源方式频数分布表
(1)频数分布表中a,b的值:a=30%;b=5;
(2)补全频数分布直方图;
(3)若全校有1000名学生,估计该校利用搜索引擎上网查找学习资源的学生有多少名?
 某学校为了了解本校学生采用何种方式上网查找所需要的学习资源,随机抽取部分学生了解情况,并将统计结果绘制成频数分布表及频数分布直方图.
某学校为了了解本校学生采用何种方式上网查找所需要的学习资源,随机抽取部分学生了解情况,并将统计结果绘制成频数分布表及频数分布直方图.上网查找学习资源方式频数分布表
| 查找方式 | 频数 | 频率 |
| 搜索引擎 | 16 | 32% |
| 专题网站 | 15 | a |
| 在线网校 | 4 | 8% |
| 试题题库 | 10 | 20% |
| 其他 | b | 10% |
(2)补全频数分布直方图;
(3)若全校有1000名学生,估计该校利用搜索引擎上网查找学习资源的学生有多少名?
 某度假村依山而建,大门A处,有一斜坡AB,长度为13米,在坡顶B处测得度假村楼CF的楼顶C的仰角∠CBF=60?,离B点8米远的E处有一花台,在E处仰望C的仰角∠CEF=73.5°,CF的延长线交校门处的水平面于D点,FD=5米.
某度假村依山而建,大门A处,有一斜坡AB,长度为13米,在坡顶B处测得度假村楼CF的楼顶C的仰角∠CBF=60?,离B点8米远的E处有一花台,在E处仰望C的仰角∠CEF=73.5°,CF的延长线交校门处的水平面于D点,FD=5米.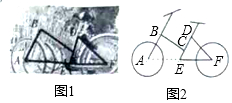 2017年初,合肥市积极推进共享单车服务(如图1),努力创造绿色环保出行,图2是某品牌单车的车架示意图,其中ED=40cm,∠DEF=60°,∠F=45°,求传动轮轴心E到后轮轴心F的距离EF的长.(结果精确到1cm,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
2017年初,合肥市积极推进共享单车服务(如图1),努力创造绿色环保出行,图2是某品牌单车的车架示意图,其中ED=40cm,∠DEF=60°,∠F=45°,求传动轮轴心E到后轮轴心F的距离EF的长.(结果精确到1cm,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
 用6个完全相同的小正方体组合成如图所示的立体图形,它的左视图为( )
用6个完全相同的小正方体组合成如图所示的立体图形,它的左视图为( )


