题目内容
3.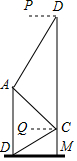 如图,某中学在教学楼前新建了一座雕塑AB,为了测量雕塑的高度,小明在二楼找到一点C,利用三角尺测得雕塑顶端点A的仰角∠QCA为45°,底部点B的俯角∠QCB为30°,小华在五楼找到一点D,利用三角尺测得点A的俯角∠PDA为60°,若AD为8m,则雕塑AB的高度为多少?(结果精确到0.1m,参考数据:$\sqrt{3}$≈1.73).
如图,某中学在教学楼前新建了一座雕塑AB,为了测量雕塑的高度,小明在二楼找到一点C,利用三角尺测得雕塑顶端点A的仰角∠QCA为45°,底部点B的俯角∠QCB为30°,小华在五楼找到一点D,利用三角尺测得点A的俯角∠PDA为60°,若AD为8m,则雕塑AB的高度为多少?(结果精确到0.1m,参考数据:$\sqrt{3}$≈1.73).
分析 过A作AR⊥DM,垂足是R,在Rt△ARD中利用三角函数求得AR的长,延长CQ交AB于点N,在Rt△ANC中利用三角函数求得AN的长,在Rt△CNB中求得NB的长,根据AB=BN+AN求解.
解答  解:过A作AR⊥DM,垂足是R.
解:过A作AR⊥DM,垂足是R.
∵∠PDA=60°,
∴∠ADR=30°,
在Rt△ARD中,AR=ADsin30°=8×$\frac{1}{2}$=4(m),
延长CQ交AB于点N.
在Rt△ANC中,∠ANC=90°,∠ACN=45°,
∴AN=NC=AR=4(m),
在Rt△CNB中,∠CNB=90°,∠NCB=30°,
∴NB=CN•tan30°=4×$\frac{\sqrt{3}}{3}$=$\frac{4\sqrt{3}}{3}$(m).
∴AB=BN+AN=$\frac{4\sqrt{3}}{3}$+4≈6.3(m).
答:雕塑AB的高约是6.3m.
点评 本题考查了解直角三角形的应用-仰角俯角问题,要求学生借助俯角构造直角三角形,并结合图形利用三角函数解直角三角形.

练习册系列答案
相关题目
16.下列计算正确的是( )
| A. | 3x2y+5xy=8x3y2 | B. | (x+y)2=x2+y2 | C. | (-2x)2÷x=4x | D. | $\frac{y}{x-y}$+$\frac{x}{y-x}$=1 |
17.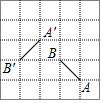 如图,在正方形网格中,线段A′B′是线段AB绕某点逆时针旋转角α得到的,点A′与A对应,则角α的大小为( )
如图,在正方形网格中,线段A′B′是线段AB绕某点逆时针旋转角α得到的,点A′与A对应,则角α的大小为( )
 如图,在正方形网格中,线段A′B′是线段AB绕某点逆时针旋转角α得到的,点A′与A对应,则角α的大小为( )
如图,在正方形网格中,线段A′B′是线段AB绕某点逆时针旋转角α得到的,点A′与A对应,则角α的大小为( )| A. | 30° | B. | 60° | C. | 90° | D. | 120° |
18.A,B,C三名学生竞选校学生会主席,他们的笔试成绩和口试成绩(单位:分)分别用了两种方式进行统计,如表一和图一:
表一:

(1)请将表一和图一中的空缺部分补充完整.
(2)竞选的最后一个程序是由本校的300名学生进行投票,A,B,C三位候选人的得票数依次为105,120,75(没有弃权票,每名学生只能推荐一个),若每票计1分,学校将笔试、口试、得票三项测试得分按4:3:3的比例确定个人成绩,请计算三位候选人的最后成绩,并根据成绩判断谁能当选.
表一:
| A | B | C | |
| 笔试 | 85 | 95 | 90 |
| 口试 | 90 | 80 | 85 |

(1)请将表一和图一中的空缺部分补充完整.
(2)竞选的最后一个程序是由本校的300名学生进行投票,A,B,C三位候选人的得票数依次为105,120,75(没有弃权票,每名学生只能推荐一个),若每票计1分,学校将笔试、口试、得票三项测试得分按4:3:3的比例确定个人成绩,请计算三位候选人的最后成绩,并根据成绩判断谁能当选.
8.(1)解方程:x2-2x=1;
(2)解不等式组:$\left\{\begin{array}{l}{x+1≥\frac{x}{2}}\\{2x+6>3x+2}\end{array}\right.$.
(2)解不等式组:$\left\{\begin{array}{l}{x+1≥\frac{x}{2}}\\{2x+6>3x+2}\end{array}\right.$.
13.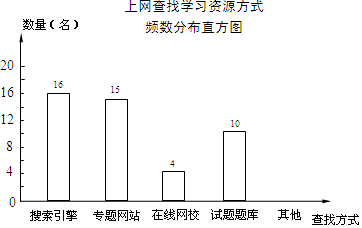 某学校为了了解本校学生采用何种方式上网查找所需要的学习资源,随机抽取部分学生了解情况,并将统计结果绘制成频数分布表及频数分布直方图.
某学校为了了解本校学生采用何种方式上网查找所需要的学习资源,随机抽取部分学生了解情况,并将统计结果绘制成频数分布表及频数分布直方图.
上网查找学习资源方式频数分布表
(1)频数分布表中a,b的值:a=30%;b=5;
(2)补全频数分布直方图;
(3)若全校有1000名学生,估计该校利用搜索引擎上网查找学习资源的学生有多少名?
 某学校为了了解本校学生采用何种方式上网查找所需要的学习资源,随机抽取部分学生了解情况,并将统计结果绘制成频数分布表及频数分布直方图.
某学校为了了解本校学生采用何种方式上网查找所需要的学习资源,随机抽取部分学生了解情况,并将统计结果绘制成频数分布表及频数分布直方图.上网查找学习资源方式频数分布表
| 查找方式 | 频数 | 频率 |
| 搜索引擎 | 16 | 32% |
| 专题网站 | 15 | a |
| 在线网校 | 4 | 8% |
| 试题题库 | 10 | 20% |
| 其他 | b | 10% |
(2)补全频数分布直方图;
(3)若全校有1000名学生,估计该校利用搜索引擎上网查找学习资源的学生有多少名?
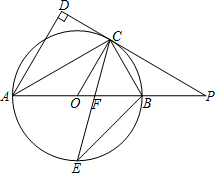 如图,AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为点D,直线DC与AB的延长线相交于点P,弦CE平分∠ACB,交AB于点F,连接BE.
如图,AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为点D,直线DC与AB的延长线相交于点P,弦CE平分∠ACB,交AB于点F,连接BE. 某度假村依山而建,大门A处,有一斜坡AB,长度为13米,在坡顶B处测得度假村楼CF的楼顶C的仰角∠CBF=60?,离B点8米远的E处有一花台,在E处仰望C的仰角∠CEF=73.5°,CF的延长线交校门处的水平面于D点,FD=5米.
某度假村依山而建,大门A处,有一斜坡AB,长度为13米,在坡顶B处测得度假村楼CF的楼顶C的仰角∠CBF=60?,离B点8米远的E处有一花台,在E处仰望C的仰角∠CEF=73.5°,CF的延长线交校门处的水平面于D点,FD=5米.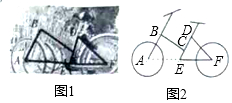 2017年初,合肥市积极推进共享单车服务(如图1),努力创造绿色环保出行,图2是某品牌单车的车架示意图,其中ED=40cm,∠DEF=60°,∠F=45°,求传动轮轴心E到后轮轴心F的距离EF的长.(结果精确到1cm,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
2017年初,合肥市积极推进共享单车服务(如图1),努力创造绿色环保出行,图2是某品牌单车的车架示意图,其中ED=40cm,∠DEF=60°,∠F=45°,求传动轮轴心E到后轮轴心F的距离EF的长.(结果精确到1cm,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)