题目内容
4. (1)解方程组$\left\{\begin{array}{l}{x+y=2}\\{2x-y=3y-2}\end{array}\right.$;
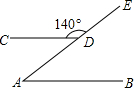
(1)解方程组$\left\{\begin{array}{l}{x+y=2}\\{2x-y=3y-2}\end{array}\right.$;(2)如图,点D在射线AE上,AB∥CD,∠CDE=140°,求∠A的度数.
分析 (1)根据代入消元法,可得方程的解;
(2)根据邻补角的性质,可得∠ADC,根据平行线的性质,可得答案.
解答  (1)解:由①得:x=-y+2③
(1)解:由①得:x=-y+2③
把③代入②得:2(-y+2)-y=3y-2
解得:y=1,
把y=1代入③得x=1,
∴方程组的解为:$\left\{\begin{array}{l}x=1\\ y=1\end{array}\right.$;
(2)解:∵∠CDE=140°,∠CDE+∠ADC=180°,
∴∠ADC=40°,
∵AB∥CD,
∴∠A=∠ADC=40°.
点评 本题考查了解二元一次方程组,解(1)的关键是代入消元法,解(2)的关键是利用平行线的性质.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
9.已知a=3b,则代数式$\frac{a+b}{a-b}$的值等于( )
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |
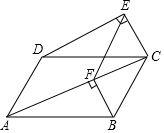 如图,已知四边形ABCD是平行四边形,∠EDC=∠CAB,∠DEC=90°.
如图,已知四边形ABCD是平行四边形,∠EDC=∠CAB,∠DEC=90°. 如图,点A、B、C在圆O上,AB为直径,且AB=4,AC=2.
如图,点A、B、C在圆O上,AB为直径,且AB=4,AC=2.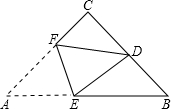 如图,在等腰Rt△ABC中,∠C=90°,D是BC的中点,将△ABC折叠,使A点与D点重合,EF为折痕.
如图,在等腰Rt△ABC中,∠C=90°,D是BC的中点,将△ABC折叠,使A点与D点重合,EF为折痕.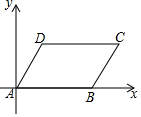 如图,在直角坐标系中,?ABCD的四个顶点的坐标分别为A(0,0),B(6,0),C (8,4),D(2,4).若直线y=3x+b把?ABCD的面积平分成相等的两部分,则b的值是-10.
如图,在直角坐标系中,?ABCD的四个顶点的坐标分别为A(0,0),B(6,0),C (8,4),D(2,4).若直线y=3x+b把?ABCD的面积平分成相等的两部分,则b的值是-10.