题目内容
20.设a是方程x2-2006x+1=0的一个根,求代数式a2-2007a+$\frac{{a}^{2}+1}{2006}$的值.分析 先把x=a代入方程,可得a2-2006a+1=0,进而可得可知a2-2006a=-1,进而可求a2-2007a=-a-1,a2+1=2006a,然后把a2-2005a与a2+1的值整体代入所求代数式求值即可.
解答 解:把x=a代入方程,可得:a2-2006a+1=0,
所以a2-2006a=-1,a2+1=2006a,
所以a2-2007a=-a-1,
所以a2-2007a+$\frac{{a}^{2}+1}{2006}$=-a-1+$\frac{2006a}{2006}$=-1,即a2-2007a+$\frac{{a}^{2}+1}{2006}$=-1.
点评 本题考查了一元二次方程的解,解题的关键是注意解与方程的关系,以及整体代入.

练习册系列答案
相关题目
12.甲.乙两车分别从A、B两地同时出发,相向而行,若快车甲的速度为60km/h,慢车乙的速度比快车甲慢4km/h,A、B两地相距80km,求两车出发到相遇所行时间.如果设xh后两车相遇,则根据题意列出方程( )
| A. | $\frac{x}{80}$+$\frac{x-4}{80}$=60 | B. | x(x-4)=80 | C. | 60x+(60-4)x=80 | D. | 60x+60(x-4)=80 |
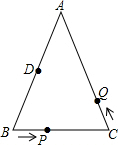 如图,△ABC中,AB=AC=12cm,BC=8cm,点D为AB的中点.如果点P在BC上以2cm/s的速度由B→C运动,同时,点Q在AC上以相同的速度由C→A运动,当点P到达点C或点Q到达点A时运动停止.
如图,△ABC中,AB=AC=12cm,BC=8cm,点D为AB的中点.如果点P在BC上以2cm/s的速度由B→C运动,同时,点Q在AC上以相同的速度由C→A运动,当点P到达点C或点Q到达点A时运动停止. 在正方形ABCD的对角线AC上取AE=AB,过E作AC的垂线交BC于F,求EF:AB的比值.
在正方形ABCD的对角线AC上取AE=AB,过E作AC的垂线交BC于F,求EF:AB的比值.