题目内容
10. 在正方形ABCD的对角线AC上取AE=AB,过E作AC的垂线交BC于F,求EF:AB的比值.
在正方形ABCD的对角线AC上取AE=AB,过E作AC的垂线交BC于F,求EF:AB的比值.
分析 连接CF,求证△AEF≌△ABF,可以求证EF=BF.进一步求证△CEF为等腰直角三角形,得出EF=CE,即可证得CF=$\sqrt{2}$EF,得出AB=BC=($\sqrt{2}$+1)EF,从而求得EF:AB的比值.
解答  解:连接AF,
解:连接AF,
在Rt△AEF和Rt△ABF中,
$\left\{\begin{array}{l}{AE=AB}\\{AF=AF}\end{array}\right.$,
∴Rt△AEF≌Rt△ABF,
∴EF=BF;
∵四边形ABCD为正方形,
∴∠ACB=45°,
在Rt△CEF中,则∠CFE=45°,
∴∠ECF=∠CFE,
∴CE=EF,
∴CE=EF=BF,
∴CF=$\sqrt{2}$EF,
∴AB=BC=($\sqrt{2}$+1)EF,
∴$\frac{EF}{AB}$=$\frac{1}{\sqrt{2}+1}$=$\sqrt{2}$-1.
点评 本题考查了正方形的性质,全等三角形的判定与性质,等腰直角三角形的判定与性质,连接CF,并且求证Rt△CEF≌Rt△CDF是解本题的关键.

练习册系列答案
相关题目
1.下列方程是一元二次方程的是( )
| A. | 3x+$\frac{1}{x}$=4 | B. | 2x(x-1)=2x2+3 | C. | x2-2=0 | D. | x+2y=1 |
5.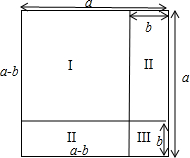 如图能验证的公式是 ( )
如图能验证的公式是 ( )
 如图能验证的公式是 ( )
如图能验证的公式是 ( )| A. | (a-b)(a+b)=a2-b2 | B. | (a+b)2=a2+2ab+b2 | C. | (a-b)2=a2-2ab+b2 | D. | a2-b2=(a-b)(a+b) |
19.有下列四个式子:①2x2+1=3x-4;②5a-b=3;③y2=1;④2t+1=7,其中是方程的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
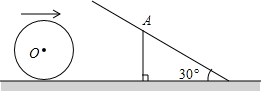 如图,桌面上有一半径为r小球向右滚动,前面有一块与桌面垂直的垂直挡板AC和一块与桌面成30°角B的斜挡板AB,两块挡板相交于点A,且有一端都紧靠桌面,如果AC=2.
如图,桌面上有一半径为r小球向右滚动,前面有一块与桌面垂直的垂直挡板AC和一块与桌面成30°角B的斜挡板AB,两块挡板相交于点A,且有一端都紧靠桌面,如果AC=2. 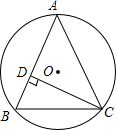 如图,△ABC内接于⊙O,半径为6,CD⊥AB于点D,sin∠ACD=$\frac{2}{3}$,则BC的长为4$\sqrt{5}$.
如图,△ABC内接于⊙O,半径为6,CD⊥AB于点D,sin∠ACD=$\frac{2}{3}$,则BC的长为4$\sqrt{5}$.