题目内容
12.甲.乙两车分别从A、B两地同时出发,相向而行,若快车甲的速度为60km/h,慢车乙的速度比快车甲慢4km/h,A、B两地相距80km,求两车出发到相遇所行时间.如果设xh后两车相遇,则根据题意列出方程( )| A. | $\frac{x}{80}$+$\frac{x-4}{80}$=60 | B. | x(x-4)=80 | C. | 60x+(60-4)x=80 | D. | 60x+60(x-4)=80 |
分析 设xh后两车相遇,根据题意可得,两车的速度和×时间=80km,据此列方程.
解答 解:设xh后两车相遇,
由题意得,60x+(60-4)x=80.
故选C.
点评 本题考查了由实际问题抽象出一元一次方程,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系,列方程.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.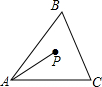 如图所示,点P为△ABC三边垂直平分线的交点,PA=6,则点P到点C的距离为PC满足( )
如图所示,点P为△ABC三边垂直平分线的交点,PA=6,则点P到点C的距离为PC满足( )
 如图所示,点P为△ABC三边垂直平分线的交点,PA=6,则点P到点C的距离为PC满足( )
如图所示,点P为△ABC三边垂直平分线的交点,PA=6,则点P到点C的距离为PC满足( )| A. | PC<6 | B. | PC=6 | C. | PC>6 | D. | 以上都不对 |
4.如图,下面是用棋子摆成的反写“T”字,按这样的规律摆下去,摆成第n个反写“T”字需要的棋子个数为( )


| A. | 3n+2 | B. | 2n+2 | C. | 3n+3 | D. | 2n+3 |
1.下列方程是一元二次方程的是( )
| A. | 3x+$\frac{1}{x}$=4 | B. | 2x(x-1)=2x2+3 | C. | x2-2=0 | D. | x+2y=1 |
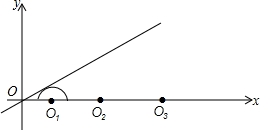 如图,圆心都在x轴正半轴上的半圆O1,半圆O2,…,半圆
如图,圆心都在x轴正半轴上的半圆O1,半圆O2,…,半圆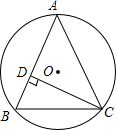 如图,△ABC内接于⊙O,半径为6,CD⊥AB于点D,sin∠ACD=$\frac{2}{3}$,则BC的长为4$\sqrt{5}$.
如图,△ABC内接于⊙O,半径为6,CD⊥AB于点D,sin∠ACD=$\frac{2}{3}$,则BC的长为4$\sqrt{5}$.