题目内容
10.试确定一元二次方程式x2-x-$\frac{1}{2}$=0的解的取值范围(精确到0.1).分析 根据公式法,可得方程的解.
解答 解:x2-x-$\frac{1}{2}$=0,
a=1,b=-1,c=-$\frac{1}{2}$.
x=$\frac{-b±\sqrt{{b}^{2}-4ac}}{2a}$=$\frac{1±\sqrt{1+2}}{2}$,
x1=$\frac{1+\sqrt{3}}{2}$≈1.4,x2=$\frac{1-\sqrt{3}}{2}$≈-0.4.
点评 本题考查了估算一元二次方程的近似解,利用公式法解方程是解题关键.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
1.对于任意有理数a,下列结论一定成立的是( )
| A. | |-a|=a | B. | (-a)2=a2 | C. | (-a)3=a3 | D. | (-a)n=an(n为正整数) |
18.长方形的周长为c米,宽为x米,则长为( )
| A. | (c-2x)米 | B. | $\frac{c-2x}{2}$米 | C. | $\frac{c-x}{2}$米 | D. | $\frac{c}{2}$-2x米 |
2.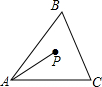 如图所示,点P为△ABC三边垂直平分线的交点,PA=6,则点P到点C的距离为PC满足( )
如图所示,点P为△ABC三边垂直平分线的交点,PA=6,则点P到点C的距离为PC满足( )
 如图所示,点P为△ABC三边垂直平分线的交点,PA=6,则点P到点C的距离为PC满足( )
如图所示,点P为△ABC三边垂直平分线的交点,PA=6,则点P到点C的距离为PC满足( )| A. | PC<6 | B. | PC=6 | C. | PC>6 | D. | 以上都不对 |