题目内容
11.作图题:如图是单位长度为1的正方形网格.(1)在图1中画出一条以格点为端点,长度为$\sqrt{8}$的线段AB;
(2)在图2中画出一个以格点为顶点,面积为10的正方形ABCD.
分析 (1)由勾股定理得出$\sqrt{{2}^{2}+{2}^{2}}$=$\sqrt{8}$=2$\sqrt{2}$,画出线段即可;
(2)由勾股定理得出$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$,画出正方形ABCD即可.
解答 解:(1)由勾股定理得: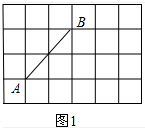
$\sqrt{{2}^{2}+{2}^{2}}$=$\sqrt{8}$=2$\sqrt{2}$,线段AB即为所求,
如图1所示:
(2)由勾股定理得:
$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$,
四边形ABCD即为所求,
如图2所示.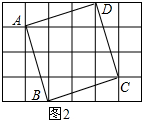
点评 本题考查了勾股定理、正方形的性质;熟练掌握勾股定理,运用勾股定理进行计算与作图是解决问题的关键.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
1.对于任意有理数a,下列结论一定成立的是( )
| A. | |-a|=a | B. | (-a)2=a2 | C. | (-a)3=a3 | D. | (-a)n=an(n为正整数) |
2.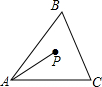 如图所示,点P为△ABC三边垂直平分线的交点,PA=6,则点P到点C的距离为PC满足( )
如图所示,点P为△ABC三边垂直平分线的交点,PA=6,则点P到点C的距离为PC满足( )
 如图所示,点P为△ABC三边垂直平分线的交点,PA=6,则点P到点C的距离为PC满足( )
如图所示,点P为△ABC三边垂直平分线的交点,PA=6,则点P到点C的距离为PC满足( )| A. | PC<6 | B. | PC=6 | C. | PC>6 | D. | 以上都不对 |
16.已知整数a1,a2,a3,a4,…满足下列条件:a1=0,a2=-|a1+1|,a3=-|a2+2|,a4=-|a3+3|,…,依此类推,则a2015的值为( )
| A. | -1005 | B. | -1006 | C. | -1007 | D. | -2014 |
1.下列方程是一元二次方程的是( )
| A. | 3x+$\frac{1}{x}$=4 | B. | 2x(x-1)=2x2+3 | C. | x2-2=0 | D. | x+2y=1 |