题目内容
11.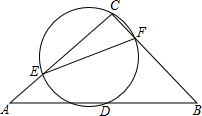 如图,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,经过C、D两点的圆交AC、BC于点E、F,且AE=CF.当圆变化时,点C到线段EF的最大距离为( )
如图,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,经过C、D两点的圆交AC、BC于点E、F,且AE=CF.当圆变化时,点C到线段EF的最大距离为( )| A. | $\sqrt{2}$ | B. | 2 | C. | $\frac{1}{2}$$\sqrt{2}$ | D. | 2$\sqrt{2}$ |
分析 连结CD、DE、DF,如图,根据等腰直角三角形的性质得∠A=45°,CD⊥AB,CD=AD=BD,∠DCB=45°,易证得△ADE≌△CDF,则∠ADE=∠CDF,DE=DF,再判断△EDF为等腰直角三角形,得到DE=$\frac{\sqrt{2}}{2}$EF,由于S△DEF=$\frac{1}{2}$•DE2=$\frac{1}{4}$EF2,所以当EF越小,S△DEF越小,加上S△CEF+S△EDF=S△ADC=$\frac{1}{2}$S△ABC,则当EF越小,S△DEF越小,而S△CEF越大,此时点C到EF的距离越大,即EF最小时,点C到EF的距离最大,设点C到EF的最大距离为h,根据圆周角定理,由∠ECF=90°得EF为⊙O的直径,所以当⊙O的直径等于CD时,⊙O的直径最小,即EF最小,此时可判断四边形CEDF为正方形,根据正方形和等腰直角三角形的性质易得h=$\sqrt{2}$.
解答  解:连结CD、DE、DF,如图,
解:连结CD、DE、DF,如图,
∵∠C=90°,AC=BC=4,
∴△ABC为等腰直角三角形,
∴∠A=45°,
∵D是AB的中点,
∴CD⊥AB,CD=AD=BD,∠DCB=45°,
在△ADE和△CDF中,
$\left\{\begin{array}{l}{AE=CF}\\{∠A=∠DCF}\\{AD=CD}\end{array}\right.$,
∴△ADE≌△CDF(SAS),
∴∠ADE=∠CDF,DE=DF,
∵∠ADF+∠CDE=90°,
∴∠CDF+∠CDE=90°,即∠EDF=90°,
∴△EDF为等腰直角三角形,
∴DE=$\frac{\sqrt{2}}{2}$EF,
∴S△DEF=$\frac{1}{2}$•DE2=$\frac{1}{4}$EF2,
当EF越小,S△DEF越小,
∵S△CEF+S△EDF=S△CDE+S△CDF=S△CED+S△ADE=S△ADC=$\frac{1}{2}$S△ABC=4,
∴当EF越小,S△DEF越小,而S△CEF越大,此时点C到EF的距离越大,
即EF最小时,点C到EF的距离最大,设点C到EF的最大距离为h,
∵∠ECF=90°,
∴EF为⊙O的直径,
∴当⊙O的直径等于CD时,⊙O的直径最小,即EF最小,此时∠DEC=∠DFC=90°,则四边形CEDF为正方形,h=$\frac{1}{2}$CD=$\frac{1}{2}$•$\frac{1}{2}$AB=$\frac{1}{2}$•$\frac{1}{2}$•4$\sqrt{2}$=$\sqrt{2}$,
即点C到线段EF的最大距离为$\sqrt{2}$.
故选A.
点评 本题考查了圆的综合题:熟练掌握圆周角定理、等腰直角三角形的性质;会运用三角形全等解决线段相等的问题;记住三角形的面积公式.

 同步练习强化拓展系列答案
同步练习强化拓展系列答案 如图是一块电脑主板的示意图,每一转角处都是直角,数据如图所示(单位:mm),则该主板的周长是( )
如图是一块电脑主板的示意图,每一转角处都是直角,数据如图所示(单位:mm),则该主板的周长是( )| A. | 88mm | B. | 96mm | C. | 80mm | D. | 84mm |
| A. | x2+2x+1=x(x+2)+1 | B. | a2-6a+9=(a-3)2 | ||
| C. | (a+1)(a-1)=a2-1 | D. | -18x4y3=-6x2y2•3x2 |
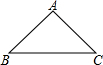 如图,已知△ABC中,AB=AC=5,BC=8.则cosB的值是( )
如图,已知△ABC中,AB=AC=5,BC=8.则cosB的值是( )| A. | 1.25 | B. | 0.8 | C. | 0.6 | D. | 0.625 |
 如图,BE、CF都是△ABC的角平分线,且∠BDC=110°,则∠A=40°.
如图,BE、CF都是△ABC的角平分线,且∠BDC=110°,则∠A=40°. 如图,已知AD∥BC,AB⊥AD,点E,F分别在射线AD,BC上.已知点E与点B关于AC对称,点E与点F关于BD对称.
如图,已知AD∥BC,AB⊥AD,点E,F分别在射线AD,BC上.已知点E与点B关于AC对称,点E与点F关于BD对称. 如图所示,在山脚C处测得山顶A仰角为30°,沿着水平地面向前300米到达点D,在D点测得山顶A的仰角为60°,求AB.
如图所示,在山脚C处测得山顶A仰角为30°,沿着水平地面向前300米到达点D,在D点测得山顶A的仰角为60°,求AB.