题目内容
19. 如图,BE、CF都是△ABC的角平分线,且∠BDC=110°,则∠A=40°.
如图,BE、CF都是△ABC的角平分线,且∠BDC=110°,则∠A=40°.
分析 根据三角形的内角和定理以及角平分线的定义,列出算式计算即可.
解答 解:∵BE、CF都是△ABC的角平分线,
∴∠A=180°-(∠ABC+∠ACB),
=180°-2(∠DBC+∠BCD)
∵∠BDC=180°-(∠DBC+∠BCD),
∴∠A=180°-2(180°-∠BDC)
∴∠BDC=90°+$\frac{1}{2}$∠A,
∴∠A=2(110°-90°)=40°.
点评 本题考查的是三角形内角和定理和角平分线的定义,用已知角表示出所求的角是解题的关键.

练习册系列答案
相关题目
14.下列不等式中,是一元一次不等式的有( )
| A. | 3x(x+5)>3x2+7 | B. | x2≥0 | C. | $\frac{1}{x}$-2<3 | D. | x+y>5 |
4. 如图,在平行四边形ABCD中,下列结论一定正确的是( )
如图,在平行四边形ABCD中,下列结论一定正确的是( )
 如图,在平行四边形ABCD中,下列结论一定正确的是( )
如图,在平行四边形ABCD中,下列结论一定正确的是( )| A. | AC⊥BD | B. | ∠A+∠B=180° | C. | AB=AD | D. | ∠A+∠C=180° |
11.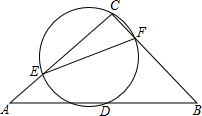 如图,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,经过C、D两点的圆交AC、BC于点E、F,且AE=CF.当圆变化时,点C到线段EF的最大距离为( )
如图,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,经过C、D两点的圆交AC、BC于点E、F,且AE=CF.当圆变化时,点C到线段EF的最大距离为( )
 如图,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,经过C、D两点的圆交AC、BC于点E、F,且AE=CF.当圆变化时,点C到线段EF的最大距离为( )
如图,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,经过C、D两点的圆交AC、BC于点E、F,且AE=CF.当圆变化时,点C到线段EF的最大距离为( )| A. | $\sqrt{2}$ | B. | 2 | C. | $\frac{1}{2}$$\sqrt{2}$ | D. | 2$\sqrt{2}$ |
8.如图,菱形ABCD中,E是AD的中点,将△CDE沿CE折叠后,点A和点D恰好重合,若菱形ABCD的面积为4$\sqrt{3}$,则菱形ABCD的周长是( )
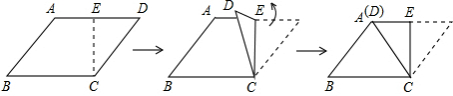

| A. | 8$\sqrt{2}$ | B. | 16$\sqrt{2}$ | C. | 8$\sqrt{3}$ | D. | 16$\sqrt{3}$ |
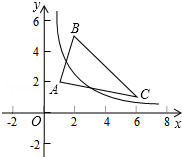 如图,△ABC的三个顶点分别为A(1,2),B(2,5),C(6,1).若函数y=$\frac{k}{x}$在第一象限内的图象与△ABC有交点,则k的取值范围是2≤k≤$\frac{49}{4}$.
如图,△ABC的三个顶点分别为A(1,2),B(2,5),C(6,1).若函数y=$\frac{k}{x}$在第一象限内的图象与△ABC有交点,则k的取值范围是2≤k≤$\frac{49}{4}$. 如图,AD是△ABC的高,BE平分∠ABC交AD于E,若∠C=70°,∠BED=64°,则∠BAC的度数为58°.
如图,AD是△ABC的高,BE平分∠ABC交AD于E,若∠C=70°,∠BED=64°,则∠BAC的度数为58°.