题目内容
16．
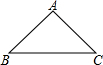如图，已知△ABC中，AB=AC=5，BC=8．则cosB的值是（ ）| A． | 1.25 | B． | 0.8 | C． | 0.6 | D． | 0.625 |
分析 作AD⊥BC于D，如图，根据等腰三角形的性质得BD=$\frac{1}{2}$BC=4，然后在Rt△ABD中利用余弦的定义求解．
解答 解：作AD⊥BC于D，如图，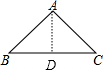
∵AB=AC=5，
∴BD=CD=$\frac{1}{2}$BC=$\frac{1}{2}$×8=4，
在Rt△ABD中，cosB=$\frac{BD}{AB}$=$\frac{4}{5}$．
故选B．
点评 本题考查了解直角三角形：在直角三角形中，由已知元素求未知元素的过程就是解直角三角形．解直角三角形要用到的关系：锐角直角的关系：∠A+∠B=90°；三边之间的关系：a2+b2=c2；边角之间的关系：锐角三角函数关系．也考查了等腰三角形的性质．
练习册系列答案
阅读快车系列答案
相关题目
4．
如图，在平行四边形ABCD中，下列结论一定正确的是（ ）
如图，在平行四边形ABCD中，下列结论一定正确的是（ ）| A． | AC⊥BD | B． | ∠A+∠B=180° | C． | AB=AD | D． | ∠A+∠C=180° |
11．
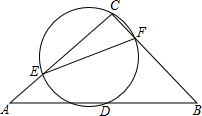如图，在△ABC中，∠C=90°，AC=BC=4，D是AB的中点，经过C、D两点的圆交AC、BC于点E、F，且AE=CF．当圆变化时，点C到线段EF的最大距离为（ ）
如图，在△ABC中，∠C=90°，AC=BC=4，D是AB的中点，经过C、D两点的圆交AC、BC于点E、F，且AE=CF．当圆变化时，点C到线段EF的最大距离为（ ）| A． | $\sqrt{2}$ | B． | 2 | C． | $\frac{1}{2}$$\sqrt{2}$ | D． | 2$\sqrt{2}$ |
1．
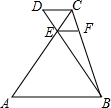如图，AB∥CD∥EF，AC与BD相交于点E，若CE=5，CF=4，AE=BC，则$\frac{CD}{AB}$的值是（ ）
如图，AB∥CD∥EF，AC与BD相交于点E，若CE=5，CF=4，AE=BC，则$\frac{CD}{AB}$的值是（ ）| A． | $\frac{2}{3}$ | B． | $\frac{1}{2}$ | C． | $\frac{1}{3}$ | D． | $\frac{1}{4}$ |
8．如图，菱形ABCD中，E是AD的中点，将△CDE沿CE折叠后，点A和点D恰好重合，若菱形ABCD的面积为4$\sqrt{3}$，则菱形ABCD的周长是（ ）
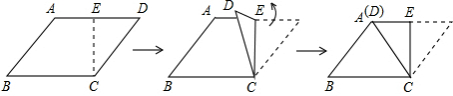
| A． | 8$\sqrt{2}$ | B． | 16$\sqrt{2}$ | C． | 8$\sqrt{3}$ | D． | 16$\sqrt{3}$ |
6．
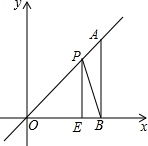如图，在平面直角坐标系中，A点为直线y=x上一点，过A点作AB⊥x轴于B点，若OB=4，E是OB边上的一点，且OE=3，点P为线段AO上的动点，则△BEP周长的最小值为（ ）
如图，在平面直角坐标系中，A点为直线y=x上一点，过A点作AB⊥x轴于B点，若OB=4，E是OB边上的一点，且OE=3，点P为线段AO上的动点，则△BEP周长的最小值为（ ）| A． | 4+2$\sqrt{2}$ | B． | 4+$\sqrt{10}$ | C． | 6 | D． | 4$\sqrt{2}$ |