题目内容
1. 如图所示,在山脚C处测得山顶A仰角为30°,沿着水平地面向前300米到达点D,在D点测得山顶A的仰角为60°,求AB.
如图所示,在山脚C处测得山顶A仰角为30°,沿着水平地面向前300米到达点D,在D点测得山顶A的仰角为60°,求AB.
分析 根据题意得∠C=30°,∠ADB=60°,CD=300米,由三角形外角的性质得到∠DAC=30°,进而根据等角对等边判定AD=CD=300米,然后在Rt△ADB中利用sin∠ADB求得AB的长即可.
解答 解:∵∠C=30°,∠ADB=60°,CD=300米,
∴∠DAC=∠ADB-∠C=30°,
∴∠C=∠DAC=30°,
∴AD=CD=300米.
∵在Rt△ABD中,∠B=90°,∠ADB=60°,
∴AB=AD•sin∠ADB=300×$\frac{\sqrt{3}}{2}$=150$\sqrt{3}$(米),
答:AB的高为150$\sqrt{3}$米.
点评 此题主要考查了解直角三角形的应用-仰角俯角问题,解题的关键是从题目中整理出直角三角形并正确的利用边角关系求解.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
11.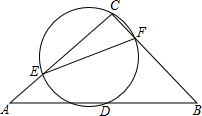 如图,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,经过C、D两点的圆交AC、BC于点E、F,且AE=CF.当圆变化时,点C到线段EF的最大距离为( )
如图,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,经过C、D两点的圆交AC、BC于点E、F,且AE=CF.当圆变化时,点C到线段EF的最大距离为( )
 如图,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,经过C、D两点的圆交AC、BC于点E、F,且AE=CF.当圆变化时,点C到线段EF的最大距离为( )
如图,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,经过C、D两点的圆交AC、BC于点E、F,且AE=CF.当圆变化时,点C到线段EF的最大距离为( )| A. | $\sqrt{2}$ | B. | 2 | C. | $\frac{1}{2}$$\sqrt{2}$ | D. | 2$\sqrt{2}$ |
6.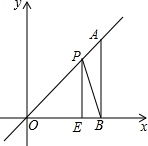 如图,在平面直角坐标系中,A点为直线y=x上一点,过A点作AB⊥x轴于B点,若OB=4,E是OB边上的一点,且OE=3,点P为线段AO上的动点,则△BEP周长的最小值为( )
如图,在平面直角坐标系中,A点为直线y=x上一点,过A点作AB⊥x轴于B点,若OB=4,E是OB边上的一点,且OE=3,点P为线段AO上的动点,则△BEP周长的最小值为( )
 如图,在平面直角坐标系中,A点为直线y=x上一点,过A点作AB⊥x轴于B点,若OB=4,E是OB边上的一点,且OE=3,点P为线段AO上的动点,则△BEP周长的最小值为( )
如图,在平面直角坐标系中,A点为直线y=x上一点,过A点作AB⊥x轴于B点,若OB=4,E是OB边上的一点,且OE=3,点P为线段AO上的动点,则△BEP周长的最小值为( )| A. | 4+2$\sqrt{2}$ | B. | 4+$\sqrt{10}$ | C. | 6 | D. | 4$\sqrt{2}$ |
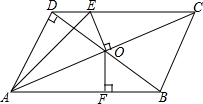 如图,在?ABCD中,BD是对角线,且BD⊥AD,OA=10cm,DB=12cm,OE⊥AC交CD于E,OF⊥AB于F
如图,在?ABCD中,BD是对角线,且BD⊥AD,OA=10cm,DB=12cm,OE⊥AC交CD于E,OF⊥AB于F