题目内容
3. 如图,已知AD∥BC,AB⊥AD,点E,F分别在射线AD,BC上.已知点E与点B关于AC对称,点E与点F关于BD对称.
如图,已知AD∥BC,AB⊥AD,点E,F分别在射线AD,BC上.已知点E与点B关于AC对称,点E与点F关于BD对称.(1)求∠DEF-∠AEB的值;
(2)tan∠ADB的值;
(3)关于点G与△BEF,你能发现什么结论?并说明理由.
分析 (1)根据轴对称的性质可得AB=AE,然后求出∠ABE=∠AEB=45°,再根据轴对称的性质可得EB=BF,BD平分∠EBF,然后求出∠FBE=45°,根据等腰三角形的两底角相等求出∠BEF=∠BFE=67.5°,再求出∠DEF=67.5°,然后代入数据计算即可得解;
(2)求出EB=ED,设AB=x,表示出AE、DE,然后求出AD,再根据锐角的正切等于对边比邻边列式计算即可得解;
(3)根据三角形的外心的定义解答.
解答 解:(1)∵点E与点B关于AC对称,
∴AB=AE,
∵AB⊥AD,
∴∠ABE=∠AEB=45°,
∵点E与点F关于BD对称,
∴EB=BF,BD平分∠EBF,
∵AD∥BC,AB⊥AD,
∴AB⊥BF,
∴∠FBE=45°,
∴∠BEF=∠BFE=67.5°,
∴∠DEF=67.5°,
∴∠DEF-∠AEB=22.5°;
(2)由(1)得∠EDB=22.5°,
∴EB=ED,
设AB=x,则AE=x,BE=DE=$\sqrt{2}$x,
∴AD=AE+DE=x+$\sqrt{2}$x,
∴tan∠ADB=$\frac{AB}{AD}$=$\frac{x}{\sqrt{2}x+x}$=$\sqrt{2}$-1;
(3)∵BD,AC分别是EF,BE的垂直平分线,
∴G是△BEF外接圆的圆心.
点评 本题考查了轴对称的性质,等腰直角三角形的判定与性质,锐角三角函数的定义,线段垂直平分线上的点到两端点的距离相等的性质,熟记各性质并准确识图,用AB表示出AD是解题的关键.

练习册系列答案
相关题目
14.下列不等式中,是一元一次不等式的有( )
| A. | 3x(x+5)>3x2+7 | B. | x2≥0 | C. | $\frac{1}{x}$-2<3 | D. | x+y>5 |
11.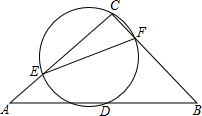 如图,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,经过C、D两点的圆交AC、BC于点E、F,且AE=CF.当圆变化时,点C到线段EF的最大距离为( )
如图,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,经过C、D两点的圆交AC、BC于点E、F,且AE=CF.当圆变化时,点C到线段EF的最大距离为( )
 如图,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,经过C、D两点的圆交AC、BC于点E、F,且AE=CF.当圆变化时,点C到线段EF的最大距离为( )
如图,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,经过C、D两点的圆交AC、BC于点E、F,且AE=CF.当圆变化时,点C到线段EF的最大距离为( )| A. | $\sqrt{2}$ | B. | 2 | C. | $\frac{1}{2}$$\sqrt{2}$ | D. | 2$\sqrt{2}$ |
8.如图,菱形ABCD中,E是AD的中点,将△CDE沿CE折叠后,点A和点D恰好重合,若菱形ABCD的面积为4$\sqrt{3}$,则菱形ABCD的周长是( )
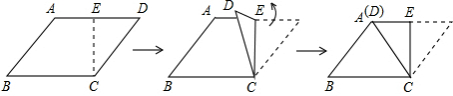

| A. | 8$\sqrt{2}$ | B. | 16$\sqrt{2}$ | C. | 8$\sqrt{3}$ | D. | 16$\sqrt{3}$ |
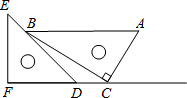 一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,AC=10,求BC、CD的长.
一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,AC=10,求BC、CD的长.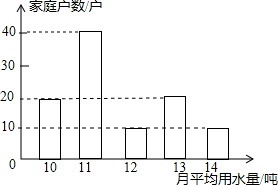 某市自来水公司对某小区500户家庭的用水情况作一次调查,随机抽查了小区100户家庭一年的越平均用水量(单位:吨),并将调查结果绘制成如图所示的条形图)
某市自来水公司对某小区500户家庭的用水情况作一次调查,随机抽查了小区100户家庭一年的越平均用水量(单位:吨),并将调查结果绘制成如图所示的条形图)