题目内容
20．解方程组：$\left\{\begin{array}{l}{2x^2-3xy+y^2-4x-3y-3=0①}\\{2x-3y=1②}\end{array}\right.$．分析 把方程②化为y=$\frac{2x-1}{3}$，代入①，得到关于x的一元二次方程，解方程求出x的值，然后求出y的值，得到方程组的解．
解答 解：由②得y=$\frac{2x-1}{3}$③，
把③代入①得，4x2-49x-17=0，
解得x=$\frac{49±9\sqrt{33}}{8}$，
把x=$\frac{49±9\sqrt{33}}{8}$代入③得，
y=$\frac{45±9\sqrt{33}}{12}$，
所以方程组的解为$\left\{\begin{array}{l}{{x}_{1}=\frac{49+9\sqrt{33}}{8}}\\{{y}_{1}=\frac{45+9\sqrt{33}}{12}}\end{array}\right.$，$\left\{\begin{array}{l}{{x}_{1}=\frac{49-9\sqrt{33}}{8}}\\{{y}_{1}=\frac{45-9\sqrt{33}}{12}}\end{array}\right.$．
点评 本题考查的是二元二次方程组的解法，正确运用代入法是解题的关键，变形其中一个方程，用一个未知数表示另一个未知数，实现消元，求出方程组的解．
练习册系列答案
相关题目
如图，AD是△ABC的高，BE平分∠ABC交AD于E，若∠C=70°，∠BED=64°，则∠BAC的度数为58°．
11．
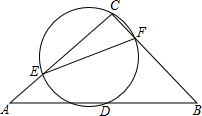如图，在△ABC中，∠C=90°，AC=BC=4，D是AB的中点，经过C、D两点的圆交AC、BC于点E、F，且AE=CF．当圆变化时，点C到线段EF的最大距离为（ ）
如图，在△ABC中，∠C=90°，AC=BC=4，D是AB的中点，经过C、D两点的圆交AC、BC于点E、F，且AE=CF．当圆变化时，点C到线段EF的最大距离为（ ）| A． | $\sqrt{2}$ | B． | 2 | C． | $\frac{1}{2}$$\sqrt{2}$ | D． | 2$\sqrt{2}$ |
8．如图，菱形ABCD中，E是AD的中点，将△CDE沿CE折叠后，点A和点D恰好重合，若菱形ABCD的面积为4$\sqrt{3}$，则菱形ABCD的周长是（ ）
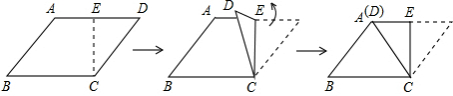
| A． | 8$\sqrt{2}$ | B． | 16$\sqrt{2}$ | C． | 8$\sqrt{3}$ | D． | 16$\sqrt{3}$ |
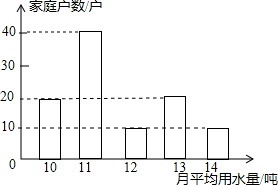某市自来水公司对某小区500户家庭的用水情况作一次调查，随机抽查了小区100户家庭一年的越平均用水量（单位：吨），并将调查结果绘制成如图所示的条形图）
