题目内容
15.先化简,再求值:$\frac{3m-9}{{m}^{2}+m}$÷($\frac{8}{m+1}$-m+1),其中m是方程x2+3x-3=0的根.分析 先算括号里面的式的减法,再算除法,根据m是方程x2+3x-3=0的根得出m2+3m=3,代入原式进行计算即可.
解答 解:根据题意知,m2+3m-3=0,
∴m2+3m=3,
原式=$\frac{3(m-3)}{m(m+1)}$÷($\frac{8}{m+1}$-$\frac{{m}^{2}-1}{m+1}$)
=$\frac{3(m-3)}{m(m+1)}$÷$\frac{9-{m}^{2}}{m+1}$
=$\frac{3(m-3)}{m(m+1)}$×$\frac{m+1}{-(m+3)(m-3)}$
=-$\frac{3}{m(m+3)}$
=-$\frac{3}{{m}^{2}+3m}$
=-$\frac{3}{3}$
=-1.
点评 本题考查的是分式的化简求值,此类题型的特点是:利用方程解的定义找到相等关系,再把所求的代数式化简后整理出所找到的相等关系的形式,再把此相等关系整体代入所求代数式,即可求出代数式的值.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
3. 如图,D是线段AB的中点,C是线段AB的垂直平分线上的一点,DE⊥AC于点E,DF⊥BC于点F.
如图,D是线段AB的中点,C是线段AB的垂直平分线上的一点,DE⊥AC于点E,DF⊥BC于点F.
(1)求证:DE=DF;
(2)当CD与AB满足怎样的数量关系时,四边形CEDF为正方形?请说明理由.
 如图,D是线段AB的中点,C是线段AB的垂直平分线上的一点,DE⊥AC于点E,DF⊥BC于点F.
如图,D是线段AB的中点,C是线段AB的垂直平分线上的一点,DE⊥AC于点E,DF⊥BC于点F.(1)求证:DE=DF;
(2)当CD与AB满足怎样的数量关系时,四边形CEDF为正方形?请说明理由.
20.一元二次方程5x2-7x+5=0的根的情况为( )
| A. | 有两个不相等的实数根 | B. | 没有实数根 | ||
| C. | 有两个相等的实数根 | D. | 只有一个实数根 |
7.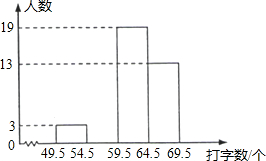 初三(1)班共有40名同学,在一次30秒打字速度测试中他们的成绩统计如表:
初三(1)班共有40名同学,在一次30秒打字速度测试中他们的成绩统计如表:
(1)将这些数据按组距5(个字)分组,绘制成如图的频数分布直方图(不完整),请将表中空缺的数据填写完整,并补全频数分布直方图;
(2)若将频数分布直方图转化为扇形统计图,则打字数在54.5-59.5这一段所在扇形的圆心角的度数是多少?
 初三(1)班共有40名同学,在一次30秒打字速度测试中他们的成绩统计如表:
初三(1)班共有40名同学,在一次30秒打字速度测试中他们的成绩统计如表:| 打字数/个 | 50 | 51 | 59 | 62 | 64 | 66 | 69 |
| 人数 | 1 | 2 | 8 | 11 | 5 |
(2)若将频数分布直方图转化为扇形统计图,则打字数在54.5-59.5这一段所在扇形的圆心角的度数是多少?
 如图,一把折扇展开后是一个扇形,其中圆心角为120°,OB=2,AB=3,则折扇纸面部分的面积为( )
如图,一把折扇展开后是一个扇形,其中圆心角为120°,OB=2,AB=3,则折扇纸面部分的面积为( ) 如图,四边形ABCD为菱形,E为对角线BD延长线上一点,且BD=4,DE=1,∠BAE=45°,则AB=2$\sqrt{10}$.
如图,四边形ABCD为菱形,E为对角线BD延长线上一点,且BD=4,DE=1,∠BAE=45°,则AB=2$\sqrt{10}$. 如图,已知△ABC,求作BC边上的高.(尺规作图,保留痕迹)
如图,已知△ABC,求作BC边上的高.(尺规作图,保留痕迹) 如图,在正方形ABCD中,AB=2,CA=CE,则△ACE的面积是2$\sqrt{2}$.
如图,在正方形ABCD中,AB=2,CA=CE,则△ACE的面积是2$\sqrt{2}$.