Question

10．如图，四边形ABCD为菱形，E为对角线BD延长线上一点，且BD=4，DE=1，∠BAE=45°，则AB=2$\sqrt{10}$．

Answer 1

分析 连接AO交BD于O，作BM⊥AE于M，交AC于N，设AM=BM=b，ME=a，想办法列出方程组求出a、b即可解决问题．

解答 解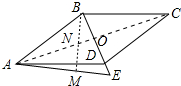：连接AO交BD于O，作BM⊥AE于M，交AC于N．
∵∠BAE=45°，∠BMA=90°，
∴∠MAB=∠MBA=45°，
∴AM=BM，
∵四边形ABCD是菱形，
∴AC⊥BD，∠AOE=90°，设AM=BM=b，ME=a，
∵∠E=∠E，∠AOE=∠BME=90°，
∴△AOE∽△BME，
∴$\frac{OE}{EM}$=$\frac{AE}{BE}$，
∴$\frac{3}{a}$=$\frac{a+b}{5}$，
∴a²+ab=15     ①
又∵a²+b²=25    ②
①×5-②×3得到：2a²+5ab-3b²=0，
∴（a+3b）（2a-b）=0，
∴b=2a代入②得到a=$\sqrt{5}$，
∴b=2$\sqrt{5}$，
∵AB=$\sqrt{2}$AM=2$\sqrt{10}$．
故答案为2$\sqrt{10}$．

点评 本题考查菱形的性质、相似三角形的判定和性质、勾股定理等知识，解题的关键是添加辅助线构造相似三角形，把问题转化为方程组解决，属于中考常考题型．