题目内容
14.观察下列等式:$\frac{1}{1×2}=1-\frac{1}{2};\frac{1}{2×3}=\frac{1}{2}-\frac{1}{3};\frac{1}{3×4}=\frac{1}{3}-\frac{1}{4};…$.以此类推!将以上面前三个等式两边分别相加,得$\frac{1}{1×2}+\frac{1}{2×3}+\frac{1}{3×4}=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}=1-\frac{1}{4}=\frac{3}{4}$;(1)猜想并写出:$\frac{1}{{n({n+1})}}$=$\frac{1}{n}$-$\frac{1}{n+1}$.
(2)根据以上规律计算:
①$\frac{1}{1×2}+\frac{1}{2×3}+\frac{1}{3×4}+…+\frac{1}{2014×2015}+\frac{1}{2015×2016}$;
②$\frac{1}{1×2}+\frac{1}{2×3}+\frac{1}{3×4}+…+\frac{1}{n×(n+1)}$.
分析 (1)归纳总结得到一般性规律,写出即可;
(2)两式利用得出的规律变形,计算即可得到结果.
解答 解:(1)根据题意得:$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$;
(2)①原式=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+…+$\frac{1}{2015}$-$\frac{1}{2016}$=1-$\frac{1}{2016}$=$\frac{2015}{2016}$;
②原式=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+…+$\frac{1}{n}$-$\frac{1}{n+1}$=1-$\frac{1}{n+1}$=$\frac{n}{n+1}$.
故答案为:(1)$\frac{1}{n}$-$\frac{1}{n+1}$
点评 此题考查了分式的加减法,弄清拆项法则是解本题的关键.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
4.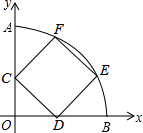 如图,以坐标原点O为圆心的圆弧交y轴于点A(0,5),交x轴于点B,正方形CDEF内接于扇形AOB(其中C在y轴上、D在x轴上,E、F在$\widehat{AB}$上),则正方形CDEF的边长为( )
如图,以坐标原点O为圆心的圆弧交y轴于点A(0,5),交x轴于点B,正方形CDEF内接于扇形AOB(其中C在y轴上、D在x轴上,E、F在$\widehat{AB}$上),则正方形CDEF的边长为( )
 如图,以坐标原点O为圆心的圆弧交y轴于点A(0,5),交x轴于点B,正方形CDEF内接于扇形AOB(其中C在y轴上、D在x轴上,E、F在$\widehat{AB}$上),则正方形CDEF的边长为( )
如图,以坐标原点O为圆心的圆弧交y轴于点A(0,5),交x轴于点B,正方形CDEF内接于扇形AOB(其中C在y轴上、D在x轴上,E、F在$\widehat{AB}$上),则正方形CDEF的边长为( )| A. | 3 | B. | $\frac{5(\sqrt{5}-1)}{2}$ | C. | $\sqrt{10}$ | D. | 以上都不正确 |
5.某工厂要建一个面积为130m2的仓库,仓库的一边靠墙(墙长为16m),并在与墙平行的一边开一道1m宽的门,现有能围成32m的木板,求仓库的长与宽?若设垂直于墙的边长为x米,则列出的方程为( )
| A. | x•(32-2x+1)=130 | B. | $\frac{{({32-2x+1})}}{2}•x=130$ | C. | x•(32-2x-1)=130 | D. | $\frac{{({32-2x-1})}}{2}•x=130$ |
19.若二次根式$\sqrt{x+1}$有意义,则x的可取的数是( )
| A. | 比1小的数 | B. | 不小于-1的数 | C. | 不大于-1的数 | D. | 全体实数 |
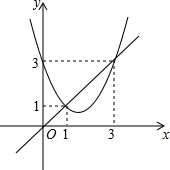 函数y=x2+bx+c与y=x的图象如图所示,有以下结论:
函数y=x2+bx+c与y=x的图象如图所示,有以下结论: